System-Level Tutorial Lesson 6: Exploring Digital Filters

What You Will Learn

In this tutorial you will learn how to use RF.Spice's black-box virtual blocks to realize different types of filters with arbitrary transfer functions.

A Note on RF.Spice's Generic Digital Filter Block

In RF.Spice A/D the generic digital filter block is defined by its Z-domain transfer function, which is a rational function of the Z-transform variable:

[math] H(z) = \frac{N(z)}{D(z)} = \frac{ \sum_{m=0}^{M} b_m z^m }{ \sum_{n=0}^{N} a_n z^n } [/math]

with the assumption that N ≥ M.

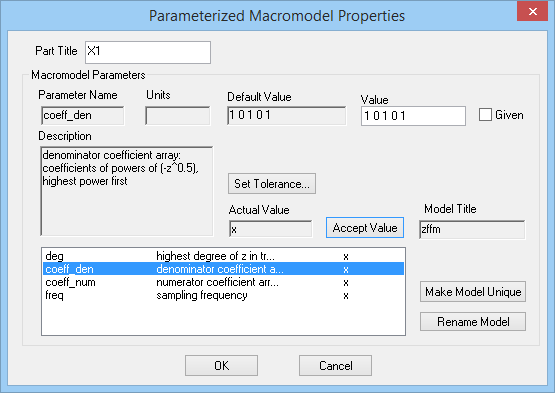
You need to specify the highest polynomial degree (N) and enter arrays of polynomial coefficients for the numerator and denominator of the transfer function in the property dialog of the generic digital filter block. This part can be accessed from Menu > Parts > Digital Signal Processing Blocks > Generic Digital Filter Block. To open the property dialog of this device, double-click on its symbol and then click the Edit Model... button.

The property dialog of the Generic Digital Filter Block: the outer dialog.

The property dialog of the Generic Digital Filter Block: the inner dialog.

For a regular digital filter, you need to insert zero padding among the numerator and denominator polynomial coefficients.

For example, the coefficient array for a polynomial P(z) = z² + z + 1 must be entered as "1 0 1 0 1". If the degree of the polynomial is N, then you need to enter a total of 2N+1 entries that include N padded zeros. The reason for this is RF.Spice A/D in fact constructs a polynomial in (-z^1/2) behind the scene. So in reality, you enter the coefficients for the successive powers of (-z^1/2):

[math] P(z) = z^2 + z + 1 = \sum_{n=0}^{N} a_n z^n = \sum_{k=0}^{2N} a^{\prime}_k (-z^{1/2})^k = 1(-z^{1/2})^4 + 0(-z^{1/2})^3 + 1(-z^{1/2})^2 + 0(-z^{1/2}) + 1 [/math]

Note that the term z^-1/2 corresponds to a delay equal to half the sampling period.

Testing a Basic Delay Element

The following is a list of parts needed for this part of the tutorial lesson:

Part Name	Part Type	Part Value
V1	Finite Sequence Pulse Generator	Waveform TBD
R1	Resistor	100
X1	Generic Digital Filter Block	Defaults, deg = 1, Numer = "1", Denom = "1 0 0", freq = 1Hz

Place and connect the part as shown in the figure below:

A simple circuit to test the generic digital filter block as a basic delay element.

In the first part of this tutorial lesson, you will define a digital filter as a basic delay element. The Z-domain transfer function of this filter is given by:

[math]H(z) = z^{-1/2} = \frac{1}{z} = \frac {0(-z^{1/2})^2 + 0(-z^{1/2}) + 1}{1(-z^{1/2})^2 + 0(-z^{1/2}) + 0} [/math]

This means that N= 1, M = 0, the coefficients of the denominator must be "1 0 0" and the numerator has only one coefficient "1". You don't have to enter the leading zero coefficients in the numerator.

As the source of your circuit, you are going to define five pulse of period 1s with a duty cycle of 20%. For this purpose, you can use a Finite Sequence Pulse Generator, which can be accessed from Parts > Waveform Generation Blocks > Basic Waveforms >. Set the pulse period to 1s, pulse width to 0.2s, n = 5, and set the rise and fall times both to 5ms.

Using pulse waveforms with zero rise or fall times in digital signal processing blocks may cause output overshoots or undershoots.

The property dialog of the Finite Sequence Pulse Generator.

Run a Transient Test of this circuit with the parameters specified below:

Start Time	0
Stop Time	8s
Linearize Step	10ms
Step Ceiling	1ms
Preset Graph Plots	v(1), v(2)

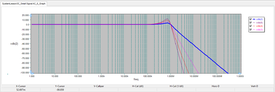
The simulation results are shown in the figure below using the graph window's Separate Plots with Vertical Tiling. You can see that the output waveform is simply the same as the delayed version of the input waveform by one clock cycle (T = 1s).

The graph of the input and output voltages of the basic delay element.

Building an FIR Filter: The Moving Average Filter

The following is a list of parts needed for this part of the tutorial lesson:

Part Name	Part Type	Part Value
V1	Random Pulse Generator	Waveform TBD
R1	Resistor	100
X1	Generic Digital Filter Block	Defaults, deg = 2, Numer = "1 0 1 0 1", Denom = "3 0 0 0 0", freq = 1Hz

One of the simplest finite impulse response (FIR) digital filters is a moving average filter. A three-point moving average filter is defined by the following transfer function:

[math]H(z) = \frac{1}{3} \left[ 1 + z^{-1} + z^{-2} \right] = \frac {z^2 + z + 1}{3z^2} [/math]

This filter sums each data sample with delayed versions of the signal by one and two clock cycles, and divides the sum by 3 to get the average. In other words, the relationship between the output and input signal can be expressed as:

[math] v_o(t) = \frac{1}{3} \left[ v_i(t) + v_i(t-T) +v_i(t-2T) \right] [/math]

where T = 1/f_c is the sampling period and f_c is the clock frequency. Therefore, M = N = 2 in the case, and the numerator and denominator coefficient arrays are "1 0 1 0 1" and "3 0 0 0 0", respectively.

Place and connect the part as shown in the above figure from the last part. For the input, this time you are going to use a random pulse generator with the parameters specified in the table below. By default, a random pulse generator create pulses with random amplitudes and random widths. The parameter n_rand determines how many possible values of amplitude or pulse width will be considered. In this project, the pulse width will be fixed at w = 0.2s, and only the pulse amplitude will be randomized. That's why you need to set the value of random_amp to 1 and set the value of random_wid to 0.

V1: Random Pulse

period	1s
duty cycle	0.2
random_amp	1
random_wid	0
n_rand	10
rise_time	1m
fall_time	1m
max_val	1V

The property dialog of the Random Pulse generator.

Run a Transient Test of this circuit with the parameters specified below:

Start Time	0
Stop Time	100s
Linearize Step	10m
Step Ceiling	1m
Preset Graph Plots	v(1), v(2)

The simulation results are shown in the figure below for the random pulse input and the filtered output signal:

The graph of the input and output voltages of the basic delay element.

---

Run an AC frequency sweep of your filter with the following parameters:

Start Frequency	1Hz
Stop Frequency	100MHz
Steps/Interval	50
Interval Type	Decade
Preset Graph Plots	Custom: Gain = VDB(2)

The frequency response is shown in the figure below as you should have expected:

The frequency response of the second-order Butterworth loswpass filter.

In this part of the tutorial lesson, create three more S-domain transfer function blocks and cascaded them as shown in the figure below. Copy and paste the additional parts since you want them to have the same properties as part A1.

The schematic of the cascaded lowpass filter using transfer function virtual blocks.

You will introduce four output voltages at Nodes 2, 3, 4 and 5. These correspond to second-order, fourth-order, sixth-order and eighth-order filter transfer functions, respectively. Note that the higher-order transfer functions realized in this way are different than the fourth-order, sixth-order and eighth-order Butterworth filter responses:

[math]H_{B4}(s) = \frac {1}{(s^2 + 0.7654s + 1)(s^2 + 1.8478s + 1)} \ne \left( \frac {1}{s^2 + 1.4142s + 1} \right)^2 [/math]

[math]H_{B6}(s) = \frac {1}{(s^2 + 0.5176s + 1)(s^2 + 1.4142s + 1)(s^2 + 1.9319s + 1)} \ne \left( \frac {1}{s^2 + 1.4142s + 1} \right)^3 [/math]

[math]H_{B8}(s) = \frac {1}{(s^2 + 0.3902s + 1)(s^2 + 1.1111s + 1)(s^2 + 1.6629s + 1)(s^2 + 1.9616s + 1)} \ne \left( \frac {1}{s^2 + 1.4142s + 1} \right)^4 [/math]

Run an AC frequency sweep of your cascaded filter with the parameters specified below:

Start Frequency	1Hz
Stop Frequency	1GHz
Steps/Interval	50
Interval Type	Decade
Preset Graph Plots	Custom: Gain = VDB(2), VDB(3), VDB(4), VDB(5)

The results are shown in the figure below:

The frequency response of the cascaded Butterworth loswpass filter.

Testing Cascaded Chebyshev Lowpass Filters

The following is a list of parts needed for this part of the tutorial lesson:

Part Name	Part Type	Part Value
V1	Voltage Source	1V
R1	Resistor	100
A1 - A4	S-Domain Transfer Function Block	Defaults

The poles of the second-order Chebyshev filter of Type I are given by:

[math] s = \pm \frac{1}{\sqrt{2}} \sinh \left( \frac{1}{2} \sinh^{-1} \left( \frac{1}{\epsilon} \right) \right) + \frac{j}{\sqrt{2}} \cosh \left( \frac{1}{2} \sinh^{-1} \left( \frac{1}{\epsilon} \right) \right)[/math]

where ε is the ripple factor. The maximum passband ripple is given by:

[math] R_{dB} = 20\log \left( \frac{1}{1/\sqrt{1+\epsilon^2}} \right) [/math]

With a ripple factor ε = 1, the maximum peak-to-peak ripples would be 3dB, and the poles are given by:

[math] s = \pm 0.3218 +j 0.7769 [/math]

The transfer function of the second-order Chebyshev filter with ε = 1 is thus given by:

[math]H(s) = \frac {1} {1.4142s^2 + 0.911s + 1} [/math]

Use the circuit of the previous part. Open the property dialog of the transfer function block A1 and change the denominator coefficients to "[1.4142 0.911 1]". Note that XSPICE process devices share the same modes. As you change the properties of A1, the properties of all the other transfer function blocks A2, A3 and A4 are updated accordingly unless you make their models unique.

Run an AC frequency sweep of your new cascaded filter with the parameters specified below:

Start Frequency	1Hz
Stop Frequency	1GHz
Steps/Interval	50
Interval Type	Decade
Preset Graph Plots	Custom: Gain = VDB(2), VDB(3), VDB(4), VDB(5)

The results are shown in the figure below:

The frequency response of the cascaded Chebyshev loswpass filter.

You can see the ripple in the passband of the filter. To better see the details, change the left axis limits to min = -10dB and max = 15dB with 5 divisions as shown in the figure below. Note that the maximum ripple of v(2) is 3dB as expected.

A close-up of the passband region of the cascaded Chebyshev loswpass filter.

Examining a Fourth-Order Chebyshev Filter

The following is a list of parts needed for this part of the tutorial lesson:

Part Name	Part Type	Part Value
V1	Voltage Source	1V
R1	Resistor	100
A1	S-Domain Transfer Function Block	Defaults

The transfer function of the fourth-order Chebyshev filter with ε = 1 is thus given by:

[math]H(s) = \frac {1} {5.65s^4 + 3.29s^3 + 6.60s^2 + 2.29s + 1} [/math]

Place and connect the part similar to the first part of this tutorial with a single block. In the property dialog of the transfer function block, set the denominator polynomial coefficients to "[5.65s 3.29 6.60 2.29 1]" and set the value of Denormalization Frequency to 6.283185Meg.

Run an AC frequency sweep of your filter with the following parameters:

Start Frequency	1Hz
Stop Frequency	100MHz
Steps/Interval	50
Interval Type	Decade
Preset Graph Plots	Custom: Gain = VDB(2)

The frequency response of the fourth-order Chebyshev filter is shown in the figure below, where you see several passband ripples. Compare this to the single ripple of the fourth-order filter in the previous section, which was made up two cascaded second-order Chebyshev filters.

The frequency response of the fourth-order Chebyshev loswpass filter.

Realizing a Second-Order Chebyshev Bandpass Filter

The following is a list of parts needed for this part of the tutorial lesson:

Part Name	Part Type	Part Value
V1	Voltage Source	1V
R1	Resistor	100
A1	S-Domain Transfer Function Block	Defaults

According to the filter theory, you can use the following transformation to realize a normalized bandpass filter from a normalized lowpass prototype:

[math] s \rightarrow \frac{1}{\Delta} \left( s + \frac{1}{s} \right) [/math]

where Δ = (ω₂ - ω₁)/ω₀ is the fractional bandwidth. If you substitute the above transformation in the second-order Chebyshev s-domain transfer function, the following transfer function is obtained:

[math]H(s) = \frac {s^2} {22.627s^4 + 3.644s^3 + 46.254s^2 + 3.644s + 22.627} [/math]

Place and connect the parts similar to the first part of this tutorial with a single block. In the property dialog of the transfer function block, set the denominator polynomial coefficients to "[22.627 3.644s 46.254 3.644 22.627]", set the numerator polynomial coefficients to "[1 0 0]", and set the value of Denormalization Frequency to 6.283185Meg.

Run an AC frequency sweep of your filter with the following parameters:

Start Frequency	1k
Stop Frequency	3MHz
Steps/Interval	1k
Interval Type	Linear
Preset Graph Plots	Custom: Gain = VDB(2)

The frequency response of the second-order Chebyshev bandpass filter is shown in the figure below. Note that a linear frequency has been chosen as opposed to the previous graphs, which had the default logarithmic X-axis scale. As you can see from the graph, the center frequency of the filter is 1MHz and its bandwidth is about 280kHz.

The frequency response of the fourth-order Chebyshev bandpass filter.

 

Back to RF.Spice A/D Tutorial Gateway