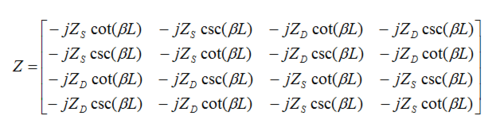RF Tutorial Lesson 6: Examining Coupled Transmission Lines
Designing a Distributed Bandpass Filter Using Coupled Lines
Contents
Objective
In this tutorial, first you will learn about RF.Spice's Generic Couple T-Lines model. Then you will cascade several sections of coupled T-Lines to design a distributed bandpas filter. Finally, you will realize a microstrip version of your distributed bandpass filter.
The Generic Coupled T-Lines Device
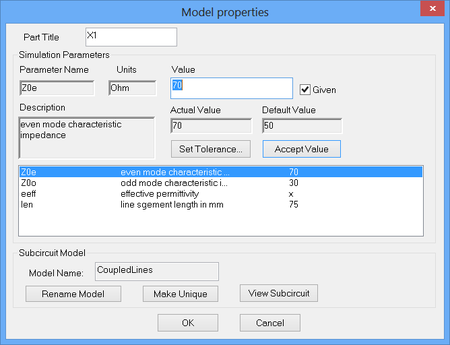
RF.Spice's Generic Couple T-Lines can be accessed from the Schematic Editor's RF Menu. It is a four-port device that models two parallel transmission line segments with equal lengths. Coupled line have several applications in RF circuit design including directional couplers, hybrids and filters. Normally you would the positive pins of the four ports and ground all the four negative pins. In RF.Spice, the generic coupled T-line device is characterized by its even and odd mode impedances, Z0e and Z0o. The system characteristic impedance of the device is defined as the geometric mean of these two impedances: Z0s = √(Z0eZ0o). Even though real physical coupled line structures have slightly different effective permittivities, the average of these two is usually taken as the effective permittivity of overall transmission line. The opposite figure shows the property dialog of the Generic Coupled T-Lines device.
Exciting the Even and Odd Modes of Coupled Lines
The following is a list of parts needed for this part of the tutorial lesson:
Two AC Voltage Sources: VS1 and VS2 (keyboard shortcut: Alt+V)
A Generic Coupled T-Line: Accessible from RF Menu
Four 50Ω Resistors: RS1, RS2, RL1 and RL2 (keyboard shortcut: R)
Two Voltage Probe Markers: VP1 and VP2 (keyboard shortcut: Alt+L)
In the analysis of coupled transmission lines, it is customary to decompose signals as the superposition of two orthogonal modes: the even and odd modes. In this part of the tutorial lesson, you will excite each of these modes. Set the values of the even and odd mode impedances of the coupled lines to Z0e = 70Ω and Z0o = 30Ω, respectively. Set the length of the lines to len = 37.5mm, which is a quarter wavelength at 2GHz assuming TEM lines (eeff = 1).
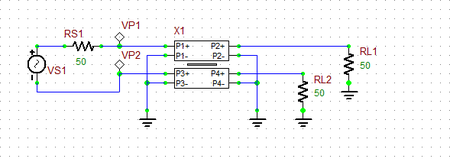
First, you will excite the even mode. Connect the two voltage sources VS1 and VS2 through the source resistors RS1 and RS2 to the positive pins of Port 1 and Port 3 of the coupled lines device, respectively. Connect the two load resistors RL1 and RL3 to the positive pins of Port 2 and Port 4 of the coupled lines device, respectively. Place voltage probe markers VP1 and VP2 at Ports 1 and 3, respectively. Run an AC Sweep Test of this circuit. Set the start and stop frequencies of the sweep to 500MHz and 3.5GHz, respectively, with a linear frequency step size of 10MHz. In the AC Sweep Test Panel, check both "Graph" and "Table" checkboxes.
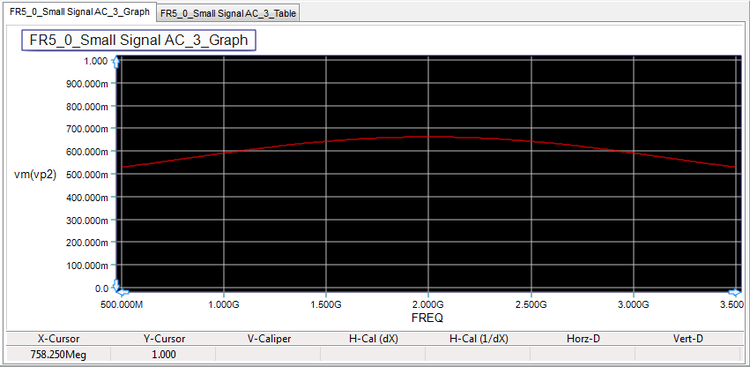
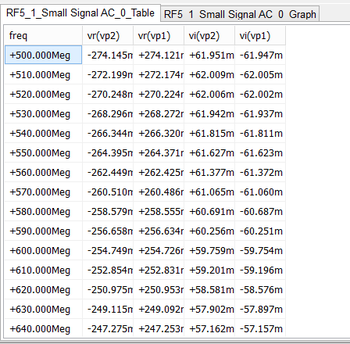
After the completion of the AC sweep, you should get a voltage graph and data table similar to the ones shown below. Note from the real/imag parts table that the two input voltages are equal.
Next, you will excite the odd mode. In this case, you will connect just a single voltage source VS1 in series with the source resistor RS1 between the positive pins of Port 1 and Port 3 of the coupled lines device as shown in the opposite figure. Connect the two load resistors RL1 and RL3 to the positive pins of Port 2 and Port 4 of the coupled lines device, respectively. Place voltage probes VP1 and VP2 at Ports 1 and 3, respectively. Run an AC Sweep Test of this circuit with the same sweep settings as in the previous case. After the completion of the AC sweep, you should get a voltage graph and data table similar to the ones shown below. This time, from the real/imag parts table you can see that the two input voltages are 180° out of phase.
Coupled Line Analysis
The Generic Coupled T-Lines device is a four-port device that can easily be analyzed based on its impedance (Z) parameters. Consider the four-port being driven from Ports 1 and 3 in the even mode, with Ports 2 and 4 terminated in two identical loads ZL. The voltage at any point on either T-Line segment can be expressed as:
[math]V_1(z) = V_2(z) = V_e^+ \left[ e^{-j\beta (z-L)} + \Gamma_{L}^e e^{j\beta (z-L)} \right] [/math]
where Ve+ is a constant, the coordinate z = 0 is assumed to be the location of Ports 1 and 3, and ΓLe is the load reflection coefficient for the even mode case:
[math]\Gamma_L^e = \frac{Z_L - Z_{0e}}{Z_L + Z_{0e}}[/math]
The input voltages VP1 and VP2 in the even mode can now be written as:
[math]V_{P1} = V_1(z=0) = V_{P2} = V_2(z=0) = V_e^+ e^{j\beta L} \left[ 1 + \Gamma_{L}^e e^{-2j\beta L} \right] [/math]
Now, let's drive the four-port from Ports 1 and 3 in the odd mode. The voltage at any point on either T-Line segment in this case can be expressed as:
[math]V_1(z) = -V_2(z) = V_o^+ \left[ e^{-j\beta z} + \Gamma_{L}^o e^{j\beta z} \right] [/math]
where Vo+ is another constant, and ΓLo is the load reflection coefficient for the odd mode case:
[math]\Gamma_L^o = \frac{Z_L - Z_{0o}}{Z_L + Z_{0o}}[/math]
The input voltages VP1 and VP2 in the odd mode can now be written as:
[math]V_{P1} = V_1(z=0) = -V_{P2} = -V_2(z=0) = V_o^+ e^{j\beta L} \left[ 1 + \Gamma_{L}^o e^{-2j\beta L} \right] [/math]
The above results can clearly be observed on the voltage graphs of the previous part, which exhibit a standing wave pattern. Note that in this case, ΓLe = (50-70)/(50+70) = -0.167 and ΓLo = (50-30)/(50+30) = 0.25. As you already saw in Tutorial Lesson 1, the exponent βL = 2πL/λg = 2π√(εeff)(f.L)/c determines the frequency variation of the voltage.
For Z-parameter calculations, we open-circuit Ports 2 and 4 (ZL = ∞). In this case, ΓLe = ΓLo = 1, and the voltages at Ports 1 and 3 now reduce to:
[math]v_1^e(0) = v_2^e(0) = 2V_e^+ cos(\beta L) = i_e Z_{in}^e [/math]
[math]v_1^o(0) = -v_2^o(0) = 2V_o^+ cos(\beta L) = i_o Z_{in}^o [/math]
where ie and io are the even and odd current at Ports 1 and 3, respectively. The total currents at Ports 1 and 3 can be expressed as (ie + io) and (ie - io), respectively. Moreover, the input impedances seen at Ports 1 and 3 in the case of even and odd excitations are given by:
[math]Z_{in}^e = -jZ_{0e} cot( \beta L) [/math]
[math]Z_{in}^o = -jZ_{0o} cot( \beta L) [/math]
Similar equations can be derived for Ports 2 and 4, when Ports 1 and 3 are open-circuited. From all these equations, one can relate the open-circuit port voltages to the port currents and finally derive the Z matrix of the four-port as follows:
where ZS = (Z0e + Z0o)/2 and ZD = (Z0e - Z0o)/2.