Difference between revisions of "Basic Principles of Physical Optics"
Kazem Sabet (Talk | contribs) (→Conventional Physical Optics (GO-PO)) |
Kazem Sabet (Talk | contribs) (→Conventional Physical Optics (GO-PO)) |
||
| Line 35: | Line 35: | ||
where it is assumed that both the incident electric field and incident magnetic field have been decomposed into two parallel and perpendicular polarizations and R<sub>||</sub> and R<sub>⊥</sub> denote the reflection coefficients at the interface between air and the impedance surface for the cases of parallel and perpendicular polarizations, respectively. These reflection coefficients are given by: | where it is assumed that both the incident electric field and incident magnetic field have been decomposed into two parallel and perpendicular polarizations and R<sub>||</sub> and R<sub>⊥</sub> denote the reflection coefficients at the interface between air and the impedance surface for the cases of parallel and perpendicular polarizations, respectively. These reflection coefficients are given by: | ||
| − | :<math> R_{\perp} = \frac{Z_s\cos\theta - | + | :<math> R_{\perp} = \frac{ \frac{Z_s}{\eta_0} \cos\theta - 1} {\frac{Z_s}{\eta_0} \cos\theta + 1} </math> |
| − | :<math> R_{\|} = \frac{ | + | :<math> R_{\|} = \frac{\cos\theta - \frac{Z_s}{\eta_0} } {\cos\theta + \frac{Z_s}{\eta_0} } </math> |
where θ is the incident angle between the propagation vector of the incident field and the normal to the surface and <math>\eta_0 = 120\pi \; \Omega</math> is the intrinsic impedance of the free space. | where θ is the incident angle between the propagation vector of the incident field and the normal to the surface and <math>\eta_0 = 120\pi \; \Omega</math> is the intrinsic impedance of the free space. | ||
Revision as of 13:17, 26 July 2018
![]() Back to Maxwell's Equations Page
Back to Maxwell's Equations Page
Contents
Physical Optics as an Asymptotic Technique
Asymptotic methods are usually valid at high frequencies as k0 R = 2π R/λ0 >> 1, where R is the distance between the source and observation points, k0 is the free-space propagation constant and λ0 is the free-space wavelength. Under such conditions, electromagnetic fields and waves start to behave more like optical fields and waves. Asymptotic methods are typically inspired by optical analysis. Two important examples of asymptotic methods are the Shoot-and-Bounce-Rays (SBR) method and Physical Optics (PO). The SBR method is a ray tracing method based on Geometrical Optics (GO) and forms the basis of the simulation engine of EM.Terrano.
In the Physical Optics (PO) method, a scatterer surface is illuminated by an incident source, and it is modeled by equivalent electric and magnetic surface currents. This concept is based on the fundamental equivalence theorem of electromagnetics. According to the Huygens principle, the equivalent electric and magnetic surface currents are derived from the tangential components of magnetic and electric fields on a given closed surface, respectively. A simple PO analysis involves only perfect electric conductors, and only electric surface currents related to the tangential magnetic fields are considered. EM.Illumina assumes that a source like a short dipole radiator or an incident plane wave induces currents on the surface of the metallic structure. These induced currents, in turn, reradiate into the free space and produce the scattered fields. In the case of an impedance surface, both surface electric and magnetic currents are induced on the surface of the scatterer.
A challenging step in establishing the PO currents is the determination of the lit and shadow points on complex scatterer geometries. The conventional physical optics method (GO-PO) uses geometrical optics ray tracing from each source to the points on the scatterers to determine whether they fall into the lit or shadow regions. But this can become a time consuming task as the size of the computational problem grows. Besides GO-PO, EM.Illumina also offers a novel Iterative Physical Optics (IPO) solver, which dispenses with the GO part of GO-PO and automatically accounts for multiple shadowing effects using an iterative algorithm.
Conventional Physical Optics (GO-PO)
The following analysis assumes a general impedance surface. The general impedance boundary condition relates the tangential components of the electric and magnetic fields on the surface:
- [math] \mathbf{\hat{n} \times E(r)} = Z_s \mathbf{\hat{n} \times \hat{n} \times H(r)} [/math]
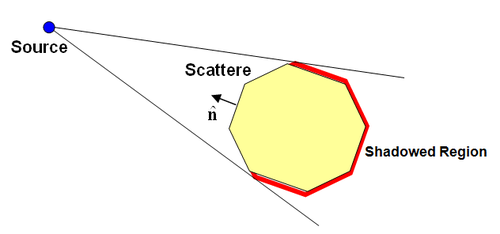
where E(r) and H(r) are the electric and magnetic fields on the surface, n is the local outward normal unit vector as shown in the figure below, and Zs is the surface impedance having units of Ohms.
To treat an object with an arbitrary geometry using PO, the object is first decomposed into many small elementary patches or cells, which have a simple geometry such as a rectangle or triangle. Then, using the tangent plane approximation, the equivalent electric and magnetic surface currents, J(r) and M(r), on the lit region of the scatterer are approximated by:
- [math] \mathbf{J(r)} = \mathbf{\hat{n}\times} \begin{bmatrix} 1+R_{||} & 0 \\ 0 & 1-R_{\perp} \end{bmatrix} \cdot \begin{bmatrix} \mathbf{H_{||}^{inc}(r)} \\ \mathbf{H_{\perp}^{inc}(r)} \end{bmatrix} [/math]
- [math] \mathbf{M(r)} = -\mathbf{\hat{n}\times} \begin{bmatrix} 1-R_{||} & 0 \\ 0 & 1+R_{\perp} \end{bmatrix} \cdot \begin{bmatrix} \mathbf{E_{||}^{inc}(r)} \\ \mathbf{E_{\perp}^{inc}(r)} \end{bmatrix} [/math]
where it is assumed that both the incident electric field and incident magnetic field have been decomposed into two parallel and perpendicular polarizations and R|| and R⊥ denote the reflection coefficients at the interface between air and the impedance surface for the cases of parallel and perpendicular polarizations, respectively. These reflection coefficients are given by:
- [math] R_{\perp} = \frac{ \frac{Z_s}{\eta_0} \cos\theta - 1} {\frac{Z_s}{\eta_0} \cos\theta + 1} [/math]
- [math] R_{\|} = \frac{\cos\theta - \frac{Z_s}{\eta_0} } {\cos\theta + \frac{Z_s}{\eta_0} } [/math]
where θ is the incident angle between the propagation vector of the incident field and the normal to the surface and [math]\eta_0 = 120\pi \; \Omega[/math] is the intrinsic impedance of the free space.
From the surface impedance boundary condition, it can easily be shown that
- [math] \mathbf{M(r)} = -Z_s \mathbf{\hat{n}\times} \mathbf{J(r)} [/math]
In the case of an impedance-matched surface (Zs = η0), one can write:
- [math] R_{\|} = -R_{\perp} = \frac{1-\cos\theta} {1+\cos\theta} [/math]
Two special limiting cases of an impedance surface are perfect electric conductor (PEC) and perfect magnetic conductor (PMC) surface. For a PEC surface, Zs = 0, R|| = R⊥ = -1, and one can write:
- [math] \mathbf{J(r)} = 2 \mathbf{\hat{n} \times H(r)} [/math]
- [math] \mathbf{M(r)} = 0 [/math]
while for a PMC surface, Zs = ∞, R|| = R⊥ = 1, and one can write:
- [math] \mathbf{J(r)} = 0 [/math]
- [math] \mathbf{M(r)} = -2 \mathbf{\hat{n} \times E(r)} [/math]
A major difficulty encountered in determining the PO currents of the scatterer is identification of lit and shadowed facets. Determination of lit and shadowed regions for simple, stand-alone, convex objects is rather simple. Denoting the incidence direction from a source to a point on the scatterer by the unit vector k, the point is considered lit if n.k< 0, and shadowed if n.k> 0. These conditions, however, are only valid if there is a direct line of sight (LOS) between the source and the centroid of the cell under consideration. They cannot predict if there are any obstructing objects in the path of the incident beam or ray. For simple convex objects, a Geometrical Optics (GO) approach can be used to finds the optical LOS lines and determine the lit and shadowed areas on the object. The conventional PO can then be used to find the electric and magnetic surface currents.
Calculating Near & Far Fields In PO
Once the electric and magnetic surface currents are determined in the lit regions of the scatterer(s), they act as secondary sources and radiate into the free space. These secondary fields are the scattered fields that are superposed with the primary incident fields. The near fields at every point r in space are calculated from:
- [math] \mathbf{ E^{tot}(r) = E^{inc}(r) } + \iint_{S_J} \mathbf{ \overline{\overline{G}}_{EJ}(r|r') \cdot J(r') } ds' + \iint_{S_M} \mathbf{ \overline{\overline{G}}_{EM}(r|r') \cdot M(r') } ds' [/math]
- [math] \mathbf{ H^{tot}(r) = H^{inc}(r) } + \iint_{S_J} \mathbf{ \overline{\overline{G}}_{HJ}(r|r') \cdot J(r') } ds' + \iint_{S_M} \mathbf{ \overline{\overline{G}}_{HM}(r|r') \cdot M(r') } ds' [/math]
where GEJ, GEM, GHJ, GHM are the dyadic Green's functions of electric and magnetic fields due to electric and magnetic currents, respectively. In EM.Illumina, the background structure is the free space. Therefore, all these dyadic Green's functions reduce to the simple free-space Green's function of the form [math]\exp(-jk_0r)/(4\pi r)[/math] and the near fields reduce to:
- [math] \begin{align} \mathbf{ E^{tot}(r) = E^{inc}(r) } & - jk_0 Z_0 \iint_{S_J} \left\{ \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{J(r')} - \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot J(r')) \hat{R} } \right\} \frac{e^{-jk_0 R}}{4\pi R} ds' \\ & + jk_0 \iint_{S_M} \left[ 1-\frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times M(r')) } \frac{e^{-jk_0 R}}{4\pi R} ds' \end{align} [/math]
- [math] \begin{align} \mathbf{ H^{tot}(r) = H^{inc}(r) } & - jk_0 Y_0 \iint_{S_M} \left\{ \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{M(r')} - \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot M(r')) \hat{R} } \right\} \frac{e^{-jk_0 R}}{4\pi R} ds' \\ & - jk_0 \iint_{S_J} \left[ 1-\frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times J(r')) } \frac{e^{-jk_0 R}}{4\pi R} ds' \end{align} [/math]
where [math]k_0 = \frac{2\pi}{\lambda_0} \text{ and } Z_0 = 1/Y_0 = \eta_0 [/math], R =r - r', R = |R|, and
- [math]\mathbf{ \hat{R} = \frac{R}{|R|} = \frac{r-r'}{|r-r'|} }[/math]
When k0r >> 1, i.e. in the far-zone field of the scatterer, one can use the asymptotic form of the Green's functions and evaluate the radiation integrals using the stationary phase method to obtain far-field expressions for the electric and magnetic fields as follows:
- [math] \mathbf{E^{ff}(r)} = \frac{jk_0 e^{-jk_0 r}}{4\pi r} \left\{ Z_0 \mathbf{ \hat{r} \times \hat{r} } \times \iint_{S_J} \mathbf{J(r')} e^{-jk_0 \mathbf{\hat{r}\cdot r'}} ds' + \mathbf{\hat{r}} \times \iint_{S_M} \mathbf{M(r')} e^{-jk_0 \mathbf{ \hat{r} \cdot r' } } ds' \right\} [/math]
- [math] \mathbf{H^{ff}(r)} = \frac{1}{Z_0} \mathbf{\hat{r} \times E^{ff}(r)} [/math]
Iterative Physical Optics (IPO)
The induced electric and magnetic surface currents on each point of the scatterer object can be calculated from the Magnetic and Electric Field Integral Equations (MFIE & EFIE):
- [math] \mathbf{J(r)} = \mathbf{\hat{n}\times} \begin{bmatrix} 1-R_{||} & 0 \\ 0 & 1-R_{\perp} \end{bmatrix} \cdot \begin{bmatrix} \mathbf{H_{||}^{tot}(r)} \\ \mathbf{H_{\perp}^{tot}(r)} \end{bmatrix} [/math]
- [math] \mathbf{M(r)} = -\mathbf{\hat{n}\times} \begin{bmatrix} 1+R_{||} & 0 \\ 0 & 1+R_{\perp} \end{bmatrix} \cdot \begin{bmatrix} \mathbf{E_{||}^{tot}(r)} \\ \mathbf{E_{\perp}^{tot}(r)} \end{bmatrix} [/math]
The shadowing phenomenon can be attributed to near-field interaction of surface currents. The current on the lit region produces a scattered field in the forward direction that is almost equal and out of phase with the incident wave. Hence, the sum of the scattered field and incident field over the shadowed region almost cancel each other, giving rise to a very small field there. This suggests that keeping track of multiple scattering can take care of shadowing problems automatically. In addition, the effects of multiple scattering can be readily accounted for by an iterative PO approach to be formulated next.
The starting point for the iterative PO solution is the above MFIE and EFIE integral equations. To the first (zero-order) approximation, we can write
- [math] \mathbf{J^{(0)}(r)} = \mathbf{\hat{n}\times} \begin{bmatrix} 1-R_{||} & 0 \\ 0 & 1-R_{\perp} \end{bmatrix} \cdot \begin{bmatrix} \mathbf{H_{||}^{inc}(r)} \\ \mathbf{H_{\perp}^{inc}(r)} \end{bmatrix} [/math]
- [math] \mathbf{M^{(0)}(r)} = -\mathbf{\hat{n}\times} \begin{bmatrix} 1+R_{||} & 0 \\ 0 & 1+R_{\perp} \end{bmatrix} \cdot \begin{bmatrix} \mathbf{E_{||}^{inc}(r)} \\ \mathbf{E_{\perp}^{inc}(r)} \end{bmatrix} [/math]
which are the conventional PO currents. However, this approximation does not formally recognize the lit and shadowed areas. Instead of identifying the exact boundaries of the lit and shadowed areas over a complex target, a simple condition is used first to find the primary shadowed areas. Then, through PO iterations all shadowed areas are determined automatically. When calculating the field on the scatterer for every source point, a primary shadowing condition given by n.k< 0 is examined. In complex scatterer geometries, there are shadowed points in concave regions where n.k> 0, but the correct shadowing is eventually achieved through the iteration of the PO currents. Therefore, in computation of the above equations, only the contribution of the points that satisfy the following condition are considered:
- [math]\mathbf{ \hat{n} \cdot \hat{R}} \lt 0 \quad \text{or} \quad \mathbf{\hat{n} \cdot (r-r')} \lt 0[/math]
At the subsequent iterations, the higher order PO currents are given by:
- [math] \mathbf{J^{(n)}(r)} = \mathbf{\hat{n}\times} \begin{bmatrix} 1-R_{||} & 0 \\ 0 & 1-R_{\perp} \end{bmatrix} \cdot \begin{bmatrix} \mathbf{H_{||}^{(n-1)}(r)} \\ \mathbf{H_{\perp}^{(n-1)}(r)} \end{bmatrix} [/math]
- [math] \mathbf{M^{(n)}(r)} = -\mathbf{\hat{n}\times} \begin{bmatrix} 1+R_{||} & 0 \\ 0 & 1+R_{\perp} \end{bmatrix} \cdot \begin{bmatrix} \mathbf{E_{||}^{(n-1)}(r)} \\ \mathbf{E_{\perp}^{(n-1)}(r)} \end{bmatrix} [/math]
For most practical applications, iterations up to the second order is sufficient. The iterative solution will not only account for double-bounce scattering over the lit regions but it also removes the lower order currents erroneously placed over concave shadowed areas.
General Huygens Sources
According to the electromagnetic equivalence theorem, if we know the tangential components of E and H fields on a closed surface, we can determine all the E and H fields inside and outside that surface in a unique way. Such a surface is called a Huygens surface. At the end of a full-wave FDTD or MoM solution, all the electric and magnetic fields are known everywhere in the computational domain. We can therefore define a box around the radiating (source) structure, over which we can record the tangential E and H field components. The tangential field components are then used to define equivalent electric and magnetic surface currents over the Huygens surface as:
- [math] \begin{align} & \mathbf{ J(r) = \hat{n} \times H(r) } \\ & \mathbf{ M(r) = -\hat{n} \times E(r) } \end{align} [/math]
In the physical optics domain, the known equivalent electric and magnetic surface currents (or indeed the known tangential E and H field components) over a given closed surface S can be used to find reradiated electric and magnetic fields everywhere in the space as follows:
- [math] \mathbf{E^{inc}(r)} = -jk_0 \sum_j \iint_{\Delta_j} \, ds' \frac{e^{-jk_0 R}}{4\pi R} \left\lbrace \begin{align} & Z_0 \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{J_j(r')} \\ & -Z_0 \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot J_j(r')) \hat{R} } \\ & - \left[ 1 - \frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times M_j(r')) } \end{align} \right\rbrace [/math]
- [math] \mathbf{H^{inc}(r)} = -jk_0 \sum_j \iint_{\Delta_j} \, ds' \frac{e^{-jk_0 R}}{4\pi R} \left\lbrace \begin{align} & Y_0 \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{M_j(r')} \\ & -Y_0 \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot M_j(r')) \hat{R} } \\ & + \left[ 1 - \frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times J_j(r')) } \end{align} \right\rbrace [/math]
where the summation over index j is carried out for all the elementary cells Δj that make up the Huygens box. In EM.Cube Huygens surfaces are cubic and are discretized using a rectangular mesh. Therefore, Δj represents any rectangular cell located on one of the six faces of Huygens box. Note that the calculated near-zone electric and magnetic fields act as incident fields for the scatterers in your EM.Illumina project. The Huygens source data are normally generated in one of EM.Cube's full-wave computational modules like FDTD, Planar or MoM3D. Keep in mind that the fields scattered (or reradiated) by your physical structure do not affect the fields inside the Huygens source.
The far fields of the Huygens surface currents are calculated from the following relations:
- [math] \mathbf{E^{ff}(r)} = \frac{jk_0}{4\pi} \frac{e^{-jk_0 r}}{r} \sum_j \iint_{\Delta_j} \left[ Z_0 \, \mathbf{ \hat{r} \times \hat{r} \times J_j(r') } + \mathbf{ \hat{r} \times M_j(r') } \right] e^{ -jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' [/math]
- [math]\mathbf{H^{ff}(r)} = \frac{1}{Z_0} \mathbf{\hat{r} \times E^{ff}(r)} [/math]