Difference between revisions of "Steady-State Thermal Analysis"
Kazem Sabet (Talk | contribs) (→Thermal Boundary Conditions) |
Kazem Sabet (Talk | contribs) |
||
| (19 intermediate revisions by the same user not shown) | |||
| Line 5: | Line 5: | ||
<tr> | <tr> | ||
</table> | </table> | ||
| + | |||
| + | [[Image:Back_icon.png|30px]] '''[[A_Review_of_Maxwell%27s_Equations_%26_Computational_Electromagnetics_(CEM) | Back to Maxwell's Equations Page]]''' | ||
| + | |||
== Heat Diffusion Equation == | == Heat Diffusion Equation == | ||
| Line 11: | Line 14: | ||
<math>q = -k\nabla T(\mathbf{r})</math> | <math>q = -k\nabla T(\mathbf{r})</math> | ||
| − | where q is the heat flux density with units of W/m<sup>2</sup>, T is the temperature expressed in °C or °K, ∇ is the gradient operator and k is the thermal conductivity with units of W/(m.K). It can be shown that the distribution of temperature is governed by the heat diffusion equation subject to the appropriate boundary conditions: | + | where q is the heat flux density with units of W/m<sup>2</sup>, T(<b>r</b>) is the temperature expressed in °C or °K, ∇ is the gradient operator and k is the thermal conductivity with units of W/(m.K). It can be shown that the distribution of temperature is governed by the heat diffusion equation subject to the appropriate boundary conditions: |
<math> \nabla^2 T(\mathbf{r}) - \frac{1} {\alpha}\frac{\partial T}{\partial t} = \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) - \frac{1} {\alpha}\frac{\partial T}{\partial t} = - \frac{w(\mathbf{r})}{k} </math> | <math> \nabla^2 T(\mathbf{r}) - \frac{1} {\alpha}\frac{\partial T}{\partial t} = \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) - \frac{1} {\alpha}\frac{\partial T}{\partial t} = - \frac{w(\mathbf{r})}{k} </math> | ||
| − | where α = k/(ρ<sub>V</sub>c<sub>p</sub>) is the thermal diffusivity with units of m<sup>2</sup>/s, ρ<sub>V</sub> is the volume mass density, c<sub>p</sub> is the specific heat capacity of the medium having units of J/(kg.K), and w(r) is the volume heat source density with units of W/m<sup>3</sup>. | + | where α = k/(ρ<sub>V</sub>c<sub>p</sub>) is the thermal diffusivity with units of m<sup>2</sup>/s, ρ<sub>V</sub> is the volume mass density having units of kg/m<sup>3</sup>, c<sub>p</sub> is the specific heat capacity of the medium having units of J/(kg.K), and w(<b>r</b>) is the volume heat source density with units of W/m<sup>3</sup>. |
In the steady-state regime, the time derivative vanishes and the diffusion equation reduces to the Poisson equation: | In the steady-state regime, the time derivative vanishes and the diffusion equation reduces to the Poisson equation: | ||
| Line 45: | Line 48: | ||
At the interface between the surface of a solid object and air, the convective boundary condition must be enforced: | At the interface between the surface of a solid object and air, the convective boundary condition must be enforced: | ||
| − | <math>-k \frac{\partial T}{\partial n} = -h \left[ T(\mathbf{r}) - T_{ | + | <math>-k \frac{\partial T}{\partial n} = -h \left[ T(\mathbf{r}) - T_{\infty} \right] </math> |
| − | where T<sub> | + | where T<sub>∞</sub> is the ambient temperature, and h is the coefficient of convective heat transfer having units of W/(m<sup>2</sup>.K). |
The convective boundary condition is a special case of Robin boundary condition: | The convective boundary condition is a special case of Robin boundary condition: | ||
| Line 53: | Line 56: | ||
<math> \left[ -k \frac{\partial T}{\partial n} + h T(\mathbf{r}) \right]_\Omega = f(\mathbf{r}) </math> | <math> \left[ -k \frac{\partial T}{\partial n} + h T(\mathbf{r}) \right]_\Omega = f(\mathbf{r}) </math> | ||
| − | where Ω is the boundary surface and f(<b>r</b>) | + | where Ω is the boundary surface and f(<b>r</b>) can be an arbitrary function in general. |
| + | |||
| + | == The Analogy between Thermal and Electrostatic Equations == | ||
| + | |||
| + | Let us now compare the steady-state thermal Poisson equation to the electrostatic Poisson equation: | ||
| + | |||
| + | <math> \nabla^2 T(\mathbf{r}) = - \frac{w(\mathbf{r})}{k} \quad \leftrightarrow \quad \nabla^2 \Phi(\mathbf{r}) = -\frac{\rho(\mathbf{r})}{\epsilon} </math> | ||
| + | |||
| + | One can see a one-to-one correspondence between the electrostatic and thermal quantities: Temperature T(<b>r</b>) is analogous to the electric scalar potential Φ(<b>r</b>), the volume heat source density w(<b>r</b>) is analogous to the volume charge density ρ(<b>r</b>), and the thermal conductivity k is analogous to the permittivity ε. | ||
| + | |||
| + | Similarly, one can establish an analogy between the heat flux <b>q</b>(<b>r</b>) and the static electric field <b>E</b>(<b>r</b>): | ||
| + | |||
| + | <math> \mathbf{q(r)} = -k\nabla T(\mathbf{r}) \quad \leftrightarrow \quad \mathbf{E(r)} = - \nabla \Phi(\mathbf{r})</math> | ||
| + | |||
| + | The table below summarizes the analogous thermal and electrical quantities: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! scope="col"| Thermal Item | ||
| + | ! scope="col"| Corresponding Electrical Item | ||
| + | |- | ||
| + | | style="width:200px;" | Temperature | ||
| + | | style="width:200px;" | Electric Scalar Potential | ||
| + | |- | ||
| + | | style="width:200px;" | Heat Flux Density | ||
| + | | style="width:200px;" | Electric Field | ||
| + | |- | ||
| + | | style="width:200px;" | Perfect Thermal Conductor | ||
| + | | style="width:200px;" | Perfect Electric Conductor | ||
| + | |- | ||
| + | | style="width:200px;" | Insulator Material | ||
| + | | style="width:200px;" | Dielectric Material | ||
| + | |- | ||
| + | | style="width:200px;" | Volume Heat Source | ||
| + | | style="width:200px;" | Volume Charge | ||
| + | |} | ||
== The Finite Difference Technique == | == The Finite Difference Technique == | ||
| − | The general form of Poisson's equation for | + | The general form of Poisson's equation for temperature can be expressed as: |
| − | <math> \frac{\partial^2 | + | <math> \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} = -f(\mathbf{r}) </math> |
When f(<b>r</b>) = 0, one obtains the well-known Laplace equation, which applies to source-free regions. | When f(<b>r</b>) = 0, one obtains the well-known Laplace equation, which applies to source-free regions. | ||
| − | The second derivative of | + | The second derivative of T with respect to the x coordinate can be approximated by the second-order difference: |
| − | <math> \frac{\partial^2 | + | <math> \frac{\partial^2 T(\mathbf{r})}{\partial x^2} \approx \frac{T(x+\Delta x,y,z)-2T(x,y,z)+T(x-\Delta x,y,z)}{(\Delta x)^2} </math> |
Similar expressions can be written for the second derivative with respect to the y and z coordinates. | Similar expressions can be written for the second derivative with respect to the y and z coordinates. | ||
| Line 79: | Line 117: | ||
</table> | </table> | ||
| − | The | + | The twmperature at the point (x,y,z) can be expressed in terms of the temperatures at its six neighboring grid points along the principal axes. This creates a 7-point computational molecule shown in the figure below: |
<table> | <table> | ||
<tr> | <tr> | ||
<td> | <td> | ||
| − | [[Image:FD | + | [[Image:FD 7PointA.png|thumb|left|480px| The 7-point computational molecule used by the finite difference solver.]] |
</td> | </td> | ||
</tr> | </tr> | ||
| Line 91: | Line 129: | ||
In the special case of a uniform grid with Δx = Δy = Δz, it can be shown that in a source-free region: | In the special case of a uniform grid with Δx = Δy = Δz, it can be shown that in a source-free region: | ||
| − | <math> | + | <math> T(i,j,k) = \frac{1}{6} \big[ T(i+1,j,k) + T(i-1,j,k) + T(i,j+1,k) + T(i,j-1,k) + T(i,j,k+1) + T(i,j,k-1) \big] </math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | The standard types of boundary conditions take the following forms: | |
| − | + | *Dirichlet boundary condition: T = T<sub>0</sub> =const. | |
| + | *Neumann boundary condition: ∂T/∂n = -q<sub>s0</sub>/k = const. | ||
| + | *Adiabatic boundary condition: ∂T/∂n = 0. | ||
| + | *Convective boundary condition: ∂T/∂n = h(T-T<sub>∞</sub>)/k. | ||
<br /> | <br /> | ||
| Line 106: | Line 142: | ||
<hr> | <hr> | ||
| − | [[Image:Top_icon.png|30px]] '''[[# | + | [[Image:Top_icon.png|30px]] '''[[#Heat_Diffusion_Equation | Back to the Top of the Page]]''' |
[[Image:Back_icon.png|30px]] '''[[A_Review_of_Maxwell%27s_Equations_%26_Computational_Electromagnetics_(CEM) | Back to Maxwell's Equations Page]]''' | [[Image:Back_icon.png|30px]] '''[[A_Review_of_Maxwell%27s_Equations_%26_Computational_Electromagnetics_(CEM) | Back to Maxwell's Equations Page]]''' | ||
Latest revision as of 21:20, 23 July 2018
![]() Back to Maxwell's Equations Page
Back to Maxwell's Equations Page
Contents
Heat Diffusion Equation
The Fourier law of heat conduction relates the heat transfer rate to the temperature variation:
[math]q = -k\nabla T(\mathbf{r})[/math]
where q is the heat flux density with units of W/m2, T(r) is the temperature expressed in °C or °K, ∇ is the gradient operator and k is the thermal conductivity with units of W/(m.K). It can be shown that the distribution of temperature is governed by the heat diffusion equation subject to the appropriate boundary conditions:
[math] \nabla^2 T(\mathbf{r}) - \frac{1} {\alpha}\frac{\partial T}{\partial t} = \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) - \frac{1} {\alpha}\frac{\partial T}{\partial t} = - \frac{w(\mathbf{r})}{k} [/math]
where α = k/(ρVcp) is the thermal diffusivity with units of m2/s, ρV is the volume mass density having units of kg/m3, cp is the specific heat capacity of the medium having units of J/(kg.K), and w(r) is the volume heat source density with units of W/m3.
In the steady-state regime, the time derivative vanishes and the diffusion equation reduces to the Poisson equation:
[math] \nabla^2 T(\mathbf{r}) = - \frac{w(\mathbf{r})}{k} [/math]
In a source-free region, the Poisson equation reduces further to the Laplace equation:
[math] \nabla^2 T(\mathbf{r}) = 0 [/math]
The steady-state heat diffusion equations are elliptic partial differential equations. These equations can be solved analytically only for a few canonical geometries with very simple boundary conditions. For most practical and realistic problems, you need to utilize a numerical technique and seek a computer solution. The Poisson and Laplace equations can be solved numerically using the finite difference (FD) method.
Thermal Boundary Conditions
The simplest thermal boundary condition at the walls of the computational domain is the Dirichlet boundary condition:
[math] T(\mathbf{r}) = T_0 [/math]
The Neumann boundary condition constrains the rate of heat flow through the domain boundary walls:
[math]-k \frac{\partial T}{\partial n} = -k \mathbf{\hat{n}} . \nabla T(\mathbf{r}) = q_s [/math]
where qs is the heat flux passing through the boundary walls.
If qs = 0, the Neumann boundary condition is also known as the adiabatic boundary condition, which represents a perfectly insulated surface:
[math]\frac{\partial T}{\partial n} = 0 [/math]
At the interface between the surface of a solid object and air, the convective boundary condition must be enforced:
[math]-k \frac{\partial T}{\partial n} = -h \left[ T(\mathbf{r}) - T_{\infty} \right] [/math]
where T∞ is the ambient temperature, and h is the coefficient of convective heat transfer having units of W/(m2.K).
The convective boundary condition is a special case of Robin boundary condition:
[math] \left[ -k \frac{\partial T}{\partial n} + h T(\mathbf{r}) \right]_\Omega = f(\mathbf{r}) [/math]
where Ω is the boundary surface and f(r) can be an arbitrary function in general.
The Analogy between Thermal and Electrostatic Equations
Let us now compare the steady-state thermal Poisson equation to the electrostatic Poisson equation:
[math] \nabla^2 T(\mathbf{r}) = - \frac{w(\mathbf{r})}{k} \quad \leftrightarrow \quad \nabla^2 \Phi(\mathbf{r}) = -\frac{\rho(\mathbf{r})}{\epsilon} [/math]
One can see a one-to-one correspondence between the electrostatic and thermal quantities: Temperature T(r) is analogous to the electric scalar potential Φ(r), the volume heat source density w(r) is analogous to the volume charge density ρ(r), and the thermal conductivity k is analogous to the permittivity ε.
Similarly, one can establish an analogy between the heat flux q(r) and the static electric field E(r):
[math] \mathbf{q(r)} = -k\nabla T(\mathbf{r}) \quad \leftrightarrow \quad \mathbf{E(r)} = - \nabla \Phi(\mathbf{r})[/math]
The table below summarizes the analogous thermal and electrical quantities:
| Thermal Item | Corresponding Electrical Item |
|---|---|
| Temperature | Electric Scalar Potential |
| Heat Flux Density | Electric Field |
| Perfect Thermal Conductor | Perfect Electric Conductor |
| Insulator Material | Dielectric Material |
| Volume Heat Source | Volume Charge |
The Finite Difference Technique
The general form of Poisson's equation for temperature can be expressed as:
[math] \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} = -f(\mathbf{r}) [/math]
When f(r) = 0, one obtains the well-known Laplace equation, which applies to source-free regions.
The second derivative of T with respect to the x coordinate can be approximated by the second-order difference:
[math] \frac{\partial^2 T(\mathbf{r})}{\partial x^2} \approx \frac{T(x+\Delta x,y,z)-2T(x,y,z)+T(x-\Delta x,y,z)}{(\Delta x)^2} [/math]
Similar expressions can be written for the second derivative with respect to the y and z coordinates.
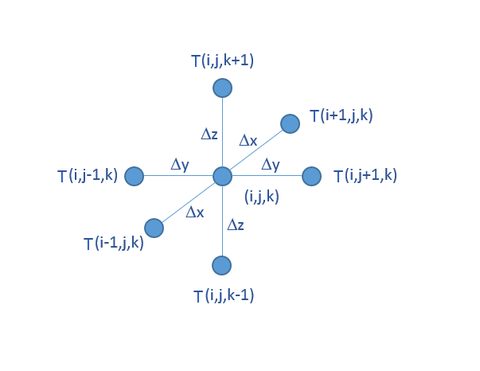
In the finite difference method, the computational domain is discretized using a 3D rectangular grid as shown on the figure below. The grid spacing along the three principal coordinate axes is denoted by Δx, Δy and Δz, respectively. In this grid, the coordinates of any point (x,y,z) in the space can be expressed as x = iΔx, y = jΔy and z = kΔz. Therefore, every point can simply be represented by an index triplet (i,j,k).
The twmperature at the point (x,y,z) can be expressed in terms of the temperatures at its six neighboring grid points along the principal axes. This creates a 7-point computational molecule shown in the figure below:
In the special case of a uniform grid with Δx = Δy = Δz, it can be shown that in a source-free region:
[math] T(i,j,k) = \frac{1}{6} \big[ T(i+1,j,k) + T(i-1,j,k) + T(i,j+1,k) + T(i,j-1,k) + T(i,j,k+1) + T(i,j,k-1) \big] [/math]
The standard types of boundary conditions take the following forms:
- Dirichlet boundary condition: T = T0 =const.
- Neumann boundary condition: ∂T/∂n = -qs0/k = const.
- Adiabatic boundary condition: ∂T/∂n = 0.
- Convective boundary condition: ∂T/∂n = h(T-T∞)/k.