Difference between revisions of "Basic Principles of SBR Ray Tracing"
Kazem Sabet (Talk | contribs) (→Physics-Based Propagation Channel Modeling Using SBR Ray Tracing) |
Kazem Sabet (Talk | contribs) |
||
| (8 intermediate revisions by the same user not shown) | |||
| Line 2: | Line 2: | ||
<table> | <table> | ||
<tr> | <tr> | ||
| − | <td>[[image:Cube-icon.png | link=Getting_Started_with_EM. | + | <td>[[image:Cube-icon.png | link=Getting_Started_with_EM.Cube]] [[image:cad-ico.png | link=Building Geometrical Constructions in CubeCAD]] [[image:fdtd-ico.png | link=EM.Tempo]] [[image:prop-ico.png | link=EM.Terrano]] [[image:static-ico.png | link=EM.Ferma]] [[image:planar-ico.png | link=EM.Picasso]] [[image:metal-ico.png | link=EM.Libera]] [[image:po-ico.png | link=EM.Illumina]] </td> |
<tr> | <tr> | ||
</table> | </table> | ||
| − | + | ||
| + | [[Image:Back_icon.png|30px]] '''[[A_Review_of_Maxwell%27s_Equations_%26_Computational_Electromagnetics_(CEM) | Back to Maxwell's Equations Page]]''' | ||
| + | |||
| + | == Physics-Based Propagation Channel Modeling == | ||
Every wireless communication system involves a transmitter that transmits some sort of signal (voice, video, data, etc.), a receiver that receives and detects the transmitted signal, and a channel in which the signal is transmitted into the air and travels from the location of the transmitter to the location of the receiver. The channel is the physical medium in which the electromagnetic waves propagate. The successful design of a communication system depends on an accurate link budget analysis that determines whether the receiver receives adequate signal power to detect it against the background noise. The simplest channel is the free space. In a free-space line-of-sight (LOS) communication system, the signal propagates directly from the transmitter to the receiver without encountering any obstacles (scatterers). Free-space line-of-sight channels are ideal scenarios that can typically be used to model aerial or space communication system applications. | Every wireless communication system involves a transmitter that transmits some sort of signal (voice, video, data, etc.), a receiver that receives and detects the transmitted signal, and a channel in which the signal is transmitted into the air and travels from the location of the transmitter to the location of the receiver. The channel is the physical medium in which the electromagnetic waves propagate. The successful design of a communication system depends on an accurate link budget analysis that determines whether the receiver receives adequate signal power to detect it against the background noise. The simplest channel is the free space. In a free-space line-of-sight (LOS) communication system, the signal propagates directly from the transmitter to the receiver without encountering any obstacles (scatterers). Free-space line-of-sight channels are ideal scenarios that can typically be used to model aerial or space communication system applications. | ||
| Line 42: | Line 45: | ||
A receiver may receive a large number of rays: direct line-of-sight rays from the transmitter, rays reflected or diffracted off the ground or terrain, rays reflected or diffracted from buildings or rays transmitted through buildings. Each received ray is characterized by its power, delay and angles of arrival, which are the spherical coordinate angles θ and φ of the incoming ray. The actual signal received and detected by the receiver is the superposition of all these rays with different power levels and different time delays. Most of the time, you will be interested in the coverage map of an area, which shows how much power is received by a grid of receivers spread over the area from a given fixed transmitter. | A receiver may receive a large number of rays: direct line-of-sight rays from the transmitter, rays reflected or diffracted off the ground or terrain, rays reflected or diffracted from buildings or rays transmitted through buildings. Each received ray is characterized by its power, delay and angles of arrival, which are the spherical coordinate angles θ and φ of the incoming ray. The actual signal received and detected by the receiver is the superposition of all these rays with different power levels and different time delays. Most of the time, you will be interested in the coverage map of an area, which shows how much power is received by a grid of receivers spread over the area from a given fixed transmitter. | ||
| − | == Ray Reflection & Transmission == | + | == Ray Reflection & Transmission in the Free Space and Inside Material Media == |
The incident, reflected and transmitted rays are each characterized by a triplet of unit vectors: | The incident, reflected and transmitted rays are each characterized by a triplet of unit vectors: | ||
| Line 63: | Line 66: | ||
:<math> \mathbf{ \hat{u}_{\|} = \hat{u}_{\perp} \times \hat{k} } </math> | :<math> \mathbf{ \hat{u}_{\|} = \hat{u}_{\perp} \times \hat{k} } </math> | ||
| − | |||
The reflected unit vectors are found as: | The reflected unit vectors are found as: | ||
| Line 72: | Line 74: | ||
:<math> \mathbf{ \hat{u}_{\|}' = \hat{u}_{\perp}' \times \hat{k}' } </math> | :<math> \mathbf{ \hat{u}_{\|}' = \hat{u}_{\perp}' \times \hat{k}' } </math> | ||
| − | |||
The transmitted unit vectors are found as: | The transmitted unit vectors are found as: | ||
| Line 81: | Line 82: | ||
:<math> \mathbf{ \hat{u}_{\|}^{\prime\prime} = \hat{u}_{\perp}^{\prime\prime} \times \hat{k}^{\prime\prime} } </math> | :<math> \mathbf{ \hat{u}_{\|}^{\prime\prime} = \hat{u}_{\perp}^{\prime\prime} \times \hat{k}^{\prime\prime} } </math> | ||
| − | |||
where | where | ||
| Line 97: | Line 97: | ||
:<math> \sin\theta^{\prime\prime} = \frac{k_1}{k_2}\sin\theta \text{ if } \sin\theta \le k_2/k_1</math> | :<math> \sin\theta^{\prime\prime} = \frac{k_1}{k_2}\sin\theta \text{ if } \sin\theta \le k_2/k_1</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The reflection coefficients at the interface are calculated for the two parallel and perpendicular polarizations as: | The reflection coefficients at the interface are calculated for the two parallel and perpendicular polarizations as: | ||
| Line 109: | Line 104: | ||
:<math> R_{\perp} = \frac { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } = \frac{\eta_2 / \cos\theta^{\prime\prime} - \eta_1 / \cos\theta} {\eta_2 / \cos\theta^{\prime\prime} + \eta_1 / \cos\theta} = \frac{Z_{2\perp} - Z_{1\perp}} {Z_{2\perp} + Z_{1\perp}} </math> | :<math> R_{\perp} = \frac { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } = \frac{\eta_2 / \cos\theta^{\prime\prime} - \eta_1 / \cos\theta} {\eta_2 / \cos\theta^{\prime\prime} + \eta_1 / \cos\theta} = \frac{Z_{2\perp} - Z_{1\perp}} {Z_{2\perp} + Z_{1\perp}} </math> | ||
| − | |||
| − | |||
== Penetration through Thin Walls or Surfaces == | == Penetration through Thin Walls or Surfaces == | ||
| Line 199: | Line 192: | ||
<hr> | <hr> | ||
| − | [[Image:Top_icon.png|30px]] '''[[# | + | [[Image:Top_icon.png|30px]] '''[[#Physics-Based_Propagation_Channel_Modeling | Back to the Top of the Page]]''' |
[[Image:Back_icon.png|30px]] '''[[A_Review_of_Maxwell%27s_Equations_%26_Computational_Electromagnetics_(CEM) | Back to Maxwell's Equations Page]]''' | [[Image:Back_icon.png|30px]] '''[[A_Review_of_Maxwell%27s_Equations_%26_Computational_Electromagnetics_(CEM) | Back to Maxwell's Equations Page]]''' | ||
| + | |||
| + | [[Image:Back_icon.png|30px]] '''[[EM.Terrano | Back to EM.Terrano Manual]]''' | ||
[[Image:Back_icon.png|30px]] '''[[EM.Cube | Back to EM.Cube Main Page]]''' | [[Image:Back_icon.png|30px]] '''[[EM.Cube | Back to EM.Cube Main Page]]''' | ||
Latest revision as of 21:19, 23 July 2018
![]() Back to Maxwell's Equations Page
Back to Maxwell's Equations Page
Contents
Physics-Based Propagation Channel Modeling
Every wireless communication system involves a transmitter that transmits some sort of signal (voice, video, data, etc.), a receiver that receives and detects the transmitted signal, and a channel in which the signal is transmitted into the air and travels from the location of the transmitter to the location of the receiver. The channel is the physical medium in which the electromagnetic waves propagate. The successful design of a communication system depends on an accurate link budget analysis that determines whether the receiver receives adequate signal power to detect it against the background noise. The simplest channel is the free space. In a free-space line-of-sight (LOS) communication system, the signal propagates directly from the transmitter to the receiver without encountering any obstacles (scatterers). Free-space line-of-sight channels are ideal scenarios that can typically be used to model aerial or space communication system applications.
Real communication channels, however, are more complicated and involve a large number of wave scatterers. For example, in an urban environment, the obstructing buildings, vehicles and vegetation reflect, diffract or attenuate the propagating radio waves. As a result, the receiver receives a distorted signal that contains several components with different power levels and different time delays arriving from different angles. The different rays arriving at a receiver location create constructive and destructive interference patterns. This is known as the multipath effect. This together with the shadowing effects caused by building obstructions lead to channel fading. The use of statistical models for prediction of fading effects is widely popular among communication system designers. These models are either based on measurement data or derived from simplistic analytical frameworks. The statistical models often exhibit considerable errors especially in areas having mixed building sizes. In such cases, one needs to perform a physics-based, site-specific analysis of the propagation environment to accurately identify and establish all the possible signal paths from the transmitter to the receiver. This involves an electromagnetic analysis of the scene with all of its geometrical and physical details.
Link budget analysis for a multipath channel is a challenging task due to the large size of the computational domains involved. Typical propagation scenes usually involve length scales on the order of thousands of wavelengths. To calculate the path loss between the transmitter and receiver, one must solve Maxwell's equations in an extremely large space. Full-wave numerical techniques like the Finite Difference Time Domain (FDTD) method, which require a fine discretization of the computational domain, are therefore impractical for solving large-scale propagation problems. The practical solution is to use asymptotic techniques such as SBR, which utilize analytical techniques over large distances rather than a brute force discretization of the entire computational domain. Such asymptotic techniques, of course, have to compromise modeling accuracy for computational efficiency.
EM.Terrano provides an asymptotic ray tracing simulation engine that is based on a technique known as Shooting-and-Bouncing-Rays (SBR). In this technique, propagating spherical waves are modeled as ray tubes or beams that emanate from a source, travel in space, bounce from obstacles and are collected by the receiver. As rays propagate away from their source (transmitter), they begin to spread (or diverge) over distance. In other words, the cross section or footprint of a ray tube expands as a function of the distance from the source. EM.Terrano uses an accurate equi-angular ray generation scheme to that produces almost identical ray tubes in all directions to satisfy energy and power conservation requirements.
Free-Space Wave Propagation
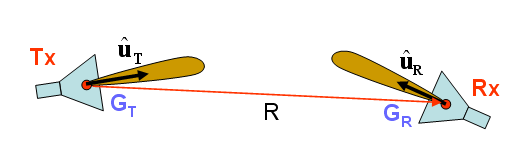
In a free-space line-of-sight (LOS) communication system, the signal propagates directly from the transmitter to the receiver without encountering any obstacles (scatterers). Electromagnetic waves propagate in the form of spherical waves with a functional dependence of ej(ωt-k0R)/R, where R is the distance between the transmitter and receiver, [math]\omega = 2\pi f[/math], f is the signal frequency, [math]k_0 = \frac{\omega}{c} = \frac{2\pi}{\lambda}[/math], c is the speed of light, and λ0 is the free-space wavelength at the operational frequency. By the time the signal arrives at the location of the receiver, it undergoes two changes. It is attenuated and its power drops by a factor of 1/R2, and additionally, it experiences a phase shift of [math]\frac{2\pi R}{\lambda_0}[/math], which is equivalent to a time delay of R/c. The signal attenuation from the transmitter to the receiver is usually quantified by Path Loss defined as the ratio of the received signal power (PR) to the transmitted signal power (PT). Assuming isotropic transmitting and receiving radiators (i.e. radiating uniformly in all directions), the Path Loss in a free-space line-of-sight communication system is given by Friis’ formula:
- [math] \frac{P_R}{P_T} = \left( \frac{\lambda_0}{4\pi R} \right)^2 [/math]
The above formula assumes that the receiving antenna is polarization-matched. Normally, there is a polarization mismatch between the transmitting and receiving antennas. In the case of directional transmitting and receiving antennas, Friis’ formula takes the following form:
- [math] P_R = P_T \, G_T G_R \left( \frac{\lambda_0}{4\pi R} \right)^2 \left| \mathbf{ \hat{u}_T \cdot \hat{u}_R } \right|^2 [/math]
where uT and uR are the unit polarization vectors of the transmitting and receiving antennas, and GT and GR are their gains, respectively.
Basic Wave Interaction Mechanisms in Ray Tracing
EM.Terrano discretizes all of the objects in your propagation scene into flat triangular facets. Obviously, rectangular and cubic objects preserve their geometric shapes through this discretization. Objects with curved surfaces such as cylinders, cones or spheres, are approximated by triangular surface mesh representations. The geometric fidelity of the resulting mesh depends on the specified mesh edge length. When a ray hits a triangular facet, the propagating spherical wave is approximated as a plane wave at the specular point. The reflection and transmission coefficients of the surface are calculated at the operational frequency and at the particular ray incident angle.
A new reflected ray is generated at the specular point, which starts traveling and bouncing around in the scene. If the obstructing surface is penetrable, a second transmitted ray is generated and added to the scene. If the ray hits the edge of an obstacle, it is diffracted from that edge. This leads to the creation of a cone of new rays, which greatly complicate the computational problem. The Uniform Theory of Diffraction (UTD) is used to calculate the wedge diffraction coefficients at the edges of scattering blocks. Note that reflection, transmission and diffraction coefficients are all dependent on the polarization of the incident plane wave.
A receiver may receive a large number of rays: direct line-of-sight rays from the transmitter, rays reflected or diffracted off the ground or terrain, rays reflected or diffracted from buildings or rays transmitted through buildings. Each received ray is characterized by its power, delay and angles of arrival, which are the spherical coordinate angles θ and φ of the incoming ray. The actual signal received and detected by the receiver is the superposition of all these rays with different power levels and different time delays. Most of the time, you will be interested in the coverage map of an area, which shows how much power is received by a grid of receivers spread over the area from a given fixed transmitter.
Ray Reflection & Transmission in the Free Space and Inside Material Media
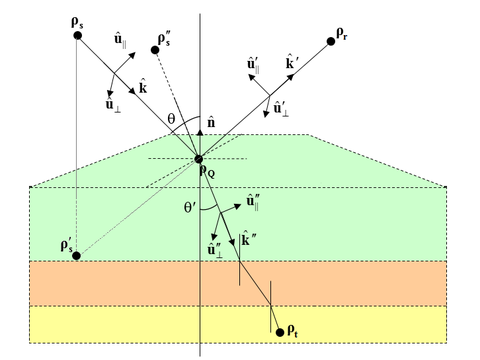
The incident, reflected and transmitted rays are each characterized by a triplet of unit vectors:
- [math]( \mathbf{ \hat{u}_{\|}, \hat{u}_{\perp}, \hat{k} } )[/math] representing the incident parallel polarization vector, incident perpendicular polarization vector and incident propagation vector, respectively.
- [math]( \mathbf{ \hat{u}_{\|}^{\prime}, \hat{u}_{\perp}', \hat{k}' } )[/math] representing the reflected parallel polarization vector, reflected perpendicular polarization vector and reflected propagation vector, respectively.
- [math]( \mathbf{ \hat{u}_{\|}^{\prime\prime}, \hat{u}_{\perp}^{\prime\prime}, \hat{k}^{\prime\prime} } )[/math] representing the transmitted parallel polarization vector, transmitted perpendicular polarization vector and transmitted propagation vector, respectively.
The reflected ray is assumed to originate from a virtual image source point. The three triplets constitute three orthonormal basis systems. Below, it is assumed that the two dielectric media have permittivities ε1 and ε2, and permeabilities μ1 and μ2, respectively. A lossy medium with a conductivity σ can be modeled by a complex permittivity εr = ε'r –jσ/ε0. Assuming n to be the unit normal to the interface plane between the two media, and Z0 = 120Ω , the incident polarization vectors as well as all the reflected and transmitted vectors are found as:
- [math] \mathbf{ \hat{u}_{\perp} = \frac{\hat{k} \times \hat{n}}{|\hat{k} \times \hat{n}|} } [/math]
- [math] \mathbf{ \hat{u}_{\|} = \hat{u}_{\perp} \times \hat{k} } [/math]
The reflected unit vectors are found as:
- [math] \mathbf{ \hat{k}' = \hat{k} - 2(\hat{k} \cdot \hat{n}) \hat{n} } [/math]
- [math] \mathbf{ \hat{u}_{\perp}' = \hat{u}_{\perp} } [/math]
- [math] \mathbf{ \hat{u}_{\|}' = \hat{u}_{\perp}' \times \hat{k}' } [/math]
The transmitted unit vectors are found as:
- [math] \mathbf{ \hat{k}^{\prime\prime} = \hat{n} \times a - \sqrt{1-a \cdot a} \; \hat{n} } [/math]
- [math] \mathbf{ \hat{u}_{\perp}^{\prime\prime} = \hat{u}_{\perp} } [/math]
- [math] \mathbf{ \hat{u}_{\|}^{\prime\prime} = \hat{u}_{\perp}^{\prime\prime} \times \hat{k}^{\prime\prime} } [/math]
where
- [math] \mathbf{a} = (k_1/k_2) \mathbf{\hat{k} \times \hat{n}}[/math]
- [math] k_1 = k_0 \sqrt{\varepsilon_1 \mu_1} [/math]
- [math] k_2 = k_0 \sqrt{\varepsilon_2 \mu_2} [/math]
- [math] \eta_1 = Z_0 \sqrt{\mu_1 / \varepsilon_1} [/math]
- [math] \eta_2 = Z_0 \sqrt{\mu_2 / \varepsilon_2} [/math]
- [math] \sin\theta^{\prime\prime} = \frac{k_1}{k_2}\sin\theta \text{ if } \sin\theta \le k_2/k_1[/math]
The reflection coefficients at the interface are calculated for the two parallel and perpendicular polarizations as:
- [math] R_{\|} = \frac { \eta_2(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) } = \frac{\eta_2 \cos\theta^{\prime\prime} - \eta_1 \cos\theta} {\eta_2 \cos\theta^{\prime\prime} + \eta_1 \cos\theta} = \frac{Z_{2\|} - Z_{1\|}} {Z_{2\|} + Z_{1\|}} [/math]
- [math] R_{\perp} = \frac { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } = \frac{\eta_2 / \cos\theta^{\prime\prime} - \eta_1 / \cos\theta} {\eta_2 / \cos\theta^{\prime\prime} + \eta_1 / \cos\theta} = \frac{Z_{2\perp} - Z_{1\perp}} {Z_{2\perp} + Z_{1\perp}} [/math]
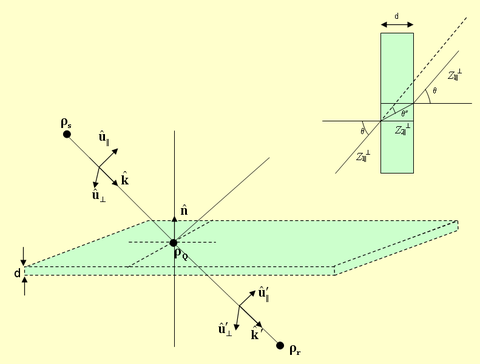
Penetration through Thin Walls or Surfaces
In "Thin Wall Approximation", we assume that an incident ray gives rise to two rays, one is reflected at the specular point, and the other is transmitted almost in the same direction as the incident ray. The reflected ray is assumed to originate from a virtual image source point. Similar to the case of reflection and transmission at the interface between two dielectric media, here too we have three triplets of unit vectors, which all form orthonormal basis systems.
The transmission coefficients are calculated for the two parallel and perpendicular polarizations as:
- [math] T_{\|} = \frac{(1-{\Gamma_{\|}}^2) \exp(-jk_2 d (\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n}}))} { 1-{\Gamma_{\|}}^2 \exp( -2jk_2 d (\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) ) } [/math]
- [math] T_{\perp} = \frac{(1-{\Gamma_{\perp}}^2) \exp(-jk_2 d (\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n}}))} { 1-{\Gamma_{\perp}}^2 \exp( -2jk_2 d (\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) ) } [/math]
where
- [math] \Gamma_{\|} = \frac{ \eta_2(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) } = \frac{\eta_2 \cos\theta^{\prime\prime} - \eta_1 \cos\theta} {\eta_2 \cos\theta^{\prime\prime} + \eta_1 \cos\theta} = \frac{Z_{2\|} - Z_{1\|}} {Z_{2\|} + Z_{1\|}} [/math]
- [math] \Gamma_{\perp} = \frac{ \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } = \frac{\eta_2 / \cos\theta^{\prime\prime} - \eta_1 / \cos\theta} {\eta_2 / \cos\theta^{\prime\prime} + \eta_1 / \cos\theta} = \frac{Z_{2\perp} - Z_{1\perp}} {Z_{2\perp} + Z_{1\perp}} [/math]
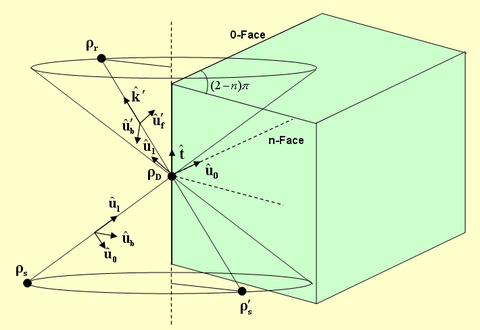
Wedge Diffraction from Edges
For the purpose of calculation of diffraction from building edges, we define a "Wedge" as having two faces, the 0-face and the n-face. The wedge angle is a = (2-n)p, where the parameter n is required for the calculation of diffraction coefficients. All the diffracted rays lie on a cone with its vertex at the diffraction point and a wedge angle equal to the angle of incidence in the opposite direction. A diffracted ray is assumed to originate from a virtual image source point. Three triplets of unit vectors are defined as follows:
- [math]\mathbf{(\hat{u}_0, \hat{u}_l, \hat{t})}[/math] representing the unit vector normal to the edge and lying in the plane of the 0-face, the unit vector normal to the 0-face, and the unit vector along the edge, respectively.
- [math]\mathbf{(\hat{u}_f, \hat{u}_b, \hat{t})}[/math] representing the incident forward polarization vector, incident backward polarization vector and incident propagation vector, respectively.
- [math]\mathbf{(\hat{u}_f', \hat{u}_b', \hat{t}')}[/math] representing the diffracted forward polarization vector, diffracted backward polarization vector and diffracted propagation vector, respectively.
The three triplets constitute three orthonormal basis systems. The propagation vector k' of the diffracted ray has to be constructed based on the diffraction cone as follows:
- [math] \mathbf{\hat{k}'} = \cos\phi_w \mathbf{\hat{u}_0} + \sin\phi_w \mathbf{\hat{u}_l} + \mathbf{(\hat{k} \cdot \hat{t}) \hat{t}}, \quad 0 \le \phi_w \le \alpha[/math]
where the resolution of the angle θw is chosen to be the same as the resolution of the incident ray.
The other unit vectors for the incident and diffracted rays are found as:
- [math] \mathbf{ \hat{u}_f = \frac{\hat{k} \times \hat{t}}{|\hat{k} \times \hat{t}|} } [/math]
- [math] \mathbf{ \hat{u}_b = \hat{k} \times \hat{u}_f } [/math]
- [math] \mathbf{ \hat{u}_f' = \frac{\hat{k}' \times \hat{t}}{|\hat{k}' \times \hat{t}|} } [/math]
- [math] \mathbf{ \hat{u}_b' = \hat{k}' \times \hat{u}_f' } [/math]
The diffraction coefficients are calculated in the following way:
- [math] D_s = \frac{-e^{-j\pi/4}}{2n \sqrt{2\pi k} \sin\beta_0'} \left\lbrace \begin{align} & \cot \left(\frac{\pi + (\phi-\phi')}{2n}\right) F[kLa^+(\phi-\phi')] + \cot \left(\frac{\pi - (\phi-\phi')}{2n}\right) F[kLa^-(\phi-\phi')] + \\ & R_{0 \perp} \cot \left(\frac{\pi - (\phi+\phi')}{2n}\right) F[kLa^-(\phi+\phi')] + R_{n \perp} \cot \left(\frac{\pi + (\phi+\phi')}{2n}\right) F[kLa^+(\phi+\phi')] \end{align} \right\rbrace [/math]
- [math] D_h = \frac{-e^{-j\pi/4}}{2n \sqrt{2\pi k} \sin\beta_0'} \left\lbrace \begin{align} & \cot \left(\frac{\pi + (\phi-\phi')}{2n}\right) F[kLa^+(\phi-\phi')] + \cot \left(\frac{\pi - (\phi-\phi')}{2n}\right) F[kLa^-(\phi-\phi')] + \\ & R_{0 \|} \cot \left(\frac{\pi - (\phi+\phi')}{2n}\right) F[kLa^-(\phi+\phi')] + R_{n \|} \cot \left(\frac{\pi + (\phi+\phi')}{2n}\right) F[kLa^+(\phi+\phi')] \end{align} \right\rbrace [/math]
where F(x) is the Fresnel Transition function:
- [math] F(x) = 2j \sqrt{x} e^{jx} \int_{\sqrt{x}}^{\infty} e^{-j\tau^2} \, d\tau [/math]
In the above equations, we have
- [math] \begin{align} s = |\rho_D - \rho_S| \\ s' = |\rho_D - \rho_r| \end{align} [/math]
- [math]L = \frac{s s' \sin^2 \beta'}{s + s'} [/math]
- [math]a^{\pm}(\nu) = 2\cos^2 \left( \frac{2n\pi N^{\pm} - \nu}{2} \right), \quad \nu = \phi \pm \phi' [/math]
where [math]N^{\pm}[/math] are the integers which most closely satisfy the equations [math] 2n\pi N^{\pm} - \nu = \pm \pi [/math].