Difference between revisions of "Application Article: Modeling Large Structures in EM.Tempo"
(→Project Setup) |
(→Project Setup) |
||
| Line 33: | Line 33: | ||
First, we create an RCS observable with 1 degree increments in both phi and theta directions. Although increasing the angular resolution of our farfield can increase simulation time, The RCS of electrically large structures tend to have very narrow peaks and nulls, so the resolution is required. | First, we create an RCS observable with 1 degree increments in both phi and theta directions. Although increasing the angular resolution of our farfield can increase simulation time, The RCS of electrically large structures tend to have very narrow peaks and nulls, so the resolution is required. | ||
| − | + | We also create two field sensors -- one with a z-normal underneath the aircraft, and another with an x-normal along the length of the aircraft. | |
[[Image:ff settings.png|thumb|left|150px|Figure 1: Geometry of the periodic unit cell of the dispersive water slab in EM.Tempo.]] | [[Image:ff settings.png|thumb|left|150px|Figure 1: Geometry of the periodic unit cell of the dispersive water slab in EM.Tempo.]] | ||
Revision as of 13:31, 10 October 2016
Introduction
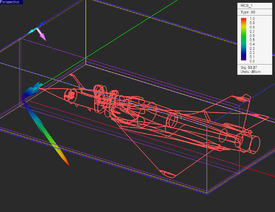
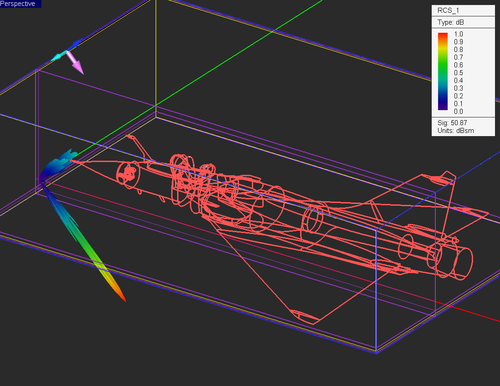
In this article, we will compute the bi-static radar cross-section (RCS) of a Dassault Mirage III type fighter aircraft at 850 MHz with EM.Tempo. Throughout the article, we will discuss a few challenges involved in working with electrically-large models.
Computational Environment
The Mirage III has approximate dimensions (length,wingspan,height) of 15m x 8m x 4.5m. Or, measured in terms of freespace wavelength at 850 MHz, 42.5 lambda x 22.66 lambda x 12.75 lambda. Thus, for the purposes of EM.Tempo, we need to solve a region of about 12,279 cubic wavelengths. For problems of this size, a great deal of CPU memory is needed, and a high-performance, multi-core CPU is desirable to reduce simulation time.
Amazon Web Services allows one to acquire high-performance compute instances on demand, and pay on a per-use basis. To be able to log into an Amazon instance via Remote Desktop Protocol, the EM.Cube license must allow terminal services (for more information, see EM.Cube Pricing). For this project, we used a c4.4xlarge instance running Windows Server 2012. This instance has 30 GiB of memory, and 16 virtual CPU cores. The CPU for this instance is an Intel Xeon E5-2666 v3 (Haswell) processor.
CAD Model
The CAD model used for this simulation was found on GrabCAD, an online repository of user-contributed CAD files and models. EM.Cube's IGES import was then used to import the model. Once we import the model, we move the Mirage to a new PEC material group in EM.Tempo.
For the present simulation, we model the entirety of the aircraft, except for the cockpit, as PEC. For the cockpit, we use EM.Cube's material database to select a glass of our choosing.
Since EM.Tempo's mesher is very robust with regard to small model inaccuracies or errors, we don't need to perform any additional healing or welding of the model.
Project Setup
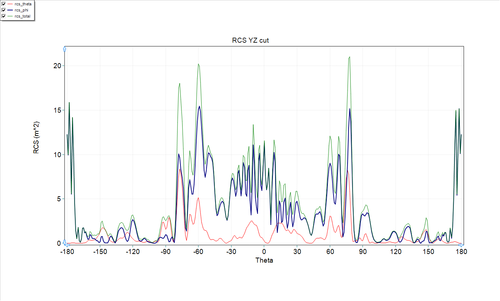
First, we create an RCS observable with 1 degree increments in both phi and theta directions. Although increasing the angular resolution of our farfield can increase simulation time, The RCS of electrically large structures tend to have very narrow peaks and nulls, so the resolution is required.
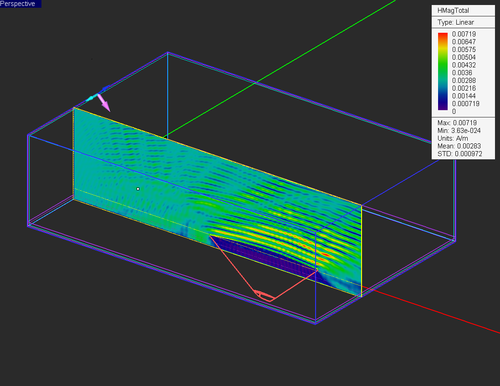
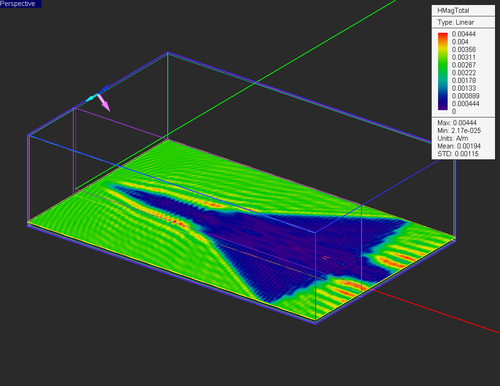
We also create two field sensors -- one with a z-normal underneath the aircraft, and another with an x-normal along the length of the aircraft.
For the mesh, we use the "Fast Run/Low Memory Settings" preset. This will set the minimum mesh rate at 15 cells per lambda, and permits grid adaptation only where necessary. This preset provides slightly less accuracy than the "High Precision Mesh Settings" preset, but results in smaller meshes, and therefore shorter run times.
Results
The complete simulation, including meshing, time-stepping, and farfield calculation took 5 hours, 50 minutes. The average performance of the timeloop was 330 MCells/s. The farfield computation requires a significant portion of the total simulation time. The farfield computation could have been reduced with larger theta and phi increments, but, typically, for electrically large structures, resolutions of 1 degree or less are required.
After the simulation is complete, the nearfield visualization are available as seen below:
270 million