Difference between revisions of "EM.Terrano"

Latest revision as of 17:59, 11 January 2021

True 3D, Coherent, Polarimetric Ray Tracer That Simulates Very Large Urban Scenes In Just Few Minutes!

EM.Terrano Tutorial Gateway

Back to EM.Cube Main Page

1 Product Overview
2 EM.Terrano Features at a Glance
3 Building a Propagation Scene in EM.Terrano
4 EM.Terrano's Ray Domain & Global Environment
- 4.1 Why Do You Need a Finite Computational Domain?
- 4.2 Understanding the Global Ground
5 Defining Point Transmitters & Point Receivers for Your Propagation Scene
6 Discretizing the Propagation Scene in EM.Terrano
- 6.1 Why Do You Need to Discretize the Scene?
- 6.2 Generating the Facet Mesh
7 Running Ray Tracing Simulations in EM.Terrano
8 Working with EM.Terrano's Simulation Data
9 Using EM.Terrano as an Asymptotic Field Solver
10 Statistical Analysis of Propagation Scene

Product Overview

EM.Terrano in a Nutshell

EM.Terrano is a physics-based, site-specific, wave propagation modeling tool that enables engineers to quickly determine how radio waves propagate in urban, natural or mixed environments. EM.Terrano's simulation engine is equipped with a fully polarimetric, coherent 3D ray tracing solver based on the Shooting-and-Bouncing-Rays (SBR) method, which utilizes geometrical optics (GO) in combination with uniform theory of diffraction (UTD) models of building edges. EM.Terrano lets you analyze and resolve all the rays transmitted from one ore more signal sources, which propagate in a real physical channel made up of buildings, terrain and other obstructing structures. EM.Terrano finds all the rays received by a receiver at a particular location in the physical site and computes their vectorial field and power levels, time delays, angles of arrival and departure, etc. Using EM.Terrano you can examine the connectivity of a communication link between any two points in a real specific propagation site.

Since its introduction in 2002, EM.Terrano has helped wireless engineers around the globe model the physical channel and the mechanisms by which radio signals propagate in various environments. EM.Terrano’s advanced ray tracing simulator finds the dominant propagation paths at each specific physical site. It calculates the true signal characteristics at the actual locations using physical databases of the buildings and terrain at a given site, not those of a statistically average or representative environment. The earlier versions of EM.Terrano's SBR solver relied on certain assumptions and approximations such as the vertical plane launch (VPL) method or 2.5D analysis of urban canyons with prismatic buildings using two separate vertical and horizontal polarizations. In 2014, we introduced a new fully 3D polarimetric SBR solver that accurately traces all the three X, Y and Z components of the electric fields (both amplitude and phase) at every point inside the computational domain. Using a 3D CAD modeler, you can now set up any number of buildings with arbitrary geometries, no longer limited to vertical prismatic shapes. Versatile interior wall arrangements allow indoor propagation modeling inside complex building configurations. The most significant recent development is a multicore parallelized SBR simulation engine that takes advantage of ultrafast k-d tree algorithms borrowed from the field of computer graphics and video gaming to achieve the ultimate speed and efficiency in geometrical optics ray tracing.

Click here to learn more about the Basic SBR Theory.

A large urban propagation scene featuring lower Manhattan.

EM.Terrano as the Propagation Module of EM.Cube

EM.Terrano is the ray tracing Propagation Module of EM.Cube, a comprehensive, integrated, modular electromagnetic modeling environment. EM.Terrano shares the visual interface, 3D parametric CAD modeler, data visualization tools, and many more utilities and features collectively known as CubeCAD with all of EM.Cube's other computational modules.

With the seamless integration of EM.Terrano with EM.Cube's other modules, you can now model complex antenna systems in EM.Tempo, EM.Libera, EM.Picasso or EM.Illumina, and generate antenna radiation patterns that can be used to model directional transmitters and receivers at the two ends of your propagation channel. Conversely, you can analyze a propagation scene in EM.Terrano, collect all the rays received at a certain receiver location and import them as coherent plane wave sources to EM.Tempo, EM.Libera, EM.Picasso or EM.Illumina.

Click here to learn more about EM.Cube Modeling Environment.

Advantages & Limitations of EM.Terrano's SBR Solver

EM.Terrano's SBR simulation engine utilizes an intelligent ray tracing algorithm that is based on the concept of k-dimensional trees. A k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are particularly useful for searches that involve multidimensional search keys such as range searches and nearest neighbor searches. In a typical large radio propagation scene, there might be a large number of rays emanating from the transmitter that may never hit any obstacles. For example, upward-looking rays in an urban propagation scene quickly exit the computational domain. Rays that hit obstacles on their path, on the other hand, generate new reflected and transmitted rays. The k-d tree algorithm traces all these rays systematically in a very fast and efficient manner. Another major advantage of k-d trees is the fast processing of multi-transmitters scenes.

EM.Terrano performs fully polarimetric and coherent SBR simulations with arbitrary transmitter antenna patterns. Its SBR simulation engine is a true asymptotic "field" solver. The amplitudes and phases of all the three vectorial field components are computed, analyzed and preserved throughout the entire ray tracing process from the source location to the field observation points. You can visualize the magnitude and phase of all six electric and magnetic field components at any point in the computational domain. In most scenes, the buildings and the ground or terrain can be assumed to be made of homogeneous materials. These are represented by their electrical properties such as permittivity ε_r and electric conductivity σ. More complex scenes may involve a multilayer ground or multilayer building walls. In such cases, one can no longer use the simple reflection or transmission coefficient formulas for homogeneous medium interfaces. EM.Terrano calculates the reflection and transmission coefficients of multilayer structures as functions of incident angle, frequency and polarization and uses them at the respective specular points.

It is very important to keep in mind that SBR is an asymptotic electromagnetic analysis technique that is based on Geometrical Optics (GO) and the Uniform Theory of Diffraction (UTD). It is not a "full-wave" technique, and it does not provide a direct numerical solution of Maxwell's equations. SBR makes a number of assumptions, chief among them, a very high operational frequency such that the length scales involved are much larger than the operating wavelength. Under this assumed regime, electromagnetic waves start to behave like optical rays. Virtually all the calculations in SBR are based on far field approximations. In order to maintain a high computational speed for urban propagation problems, EM.Terrano ignores double diffractions. Diffractions from edges give rise to a large number of new secondary rays. The power of diffracted rays drops much faster than reflected rays. In other words, an edge-diffracted ray does not diffract again from another edge in EM.Terrano. However, reflected and penetrated rays do get diffracted from edges just as rays emanated directly from the sources do.

A multipath urban propagation scene showing all the rays collected by a receiver.

EM.Terrano Features at a Glance

Scene Definition / Construction

Buildings/blocks with arbitrary geometries and material properties
Buildings/blocks with impenetrable surfaces or penetrable surfaces using thin wall approximation
Multilayer walls for indoor propagation scenes
Penetrable volume blocks with arbitrary geometries and material properties
Import of shapefiles and STEP, IGES and STL CAD model files for scene construction
Terrain surfaces with arbitrary geometries and material properties and random rough surface profiles
Import of digital elevation map (DEM) terrain models
Python-based random city wizard with randomized building locations, extents and orientations
Python-based wizards for generation of parameterized multi-story office buildings and several terrain scene types
Standard half-wave dipole transmitters and receivers oriented along the principal axes
Short Hertzian dipole sources with arbitrary orientation
Isotropic receivers or receiver grids for wireless coverage modeling
Radiator sets with 3D directional antenna patterns (imported from other modules or external files)
Full three-axis rotation of imported antenna patterns
Interchangeable radiator-based definition of transmitters and receivers (networks of transceivers)

Wave Propagation Modeling

Fully 3D polarimetric and coherent Shoot-and-Bounce-Rays (SBR) simulation engine
GTD/UTD diffraction models for diffraction from building edges and terrain
Triangular surface mesh generator for discretization of arbitrary block geometries
Super-fast geometrical/optical ray tracing using advanced k-d tree algorithms
Intelligent ray tracing with user defined angular extents and resolution
Ray reflection, edge diffraction and ray transmission through multilayer walls and material volumes
Communication link analysis for superheterodyne transmitters and receivers
17 digital modulation waveforms for the calculation of E_b/N₀ and Bit error rate (BER)
Incredibly fast frequency sweeps of the entire propagation scene in a single SBR simulation run
Parametric sweeps of scene elements like building properties, or radiator heights and rotation angles
Statistical analysis of the propagation scene
Polarimetric channel characterization for MIMO analysis
"Almost real-time" Polarimatrix solver using an existing ray database
"Almost real-time" transmitter sweep using the Polarimatrix solver
"Almost real-time" rotational sweep for modeling beam steering using the Polarimatrix solver
"Almost real-time" mobile sweep for modeling mobile communications between Tx-Rx pairs along a mobile path using the Polarimatrix solver

Data Generation & Visualization

Standard output parameters for received power, path loss, SNR, E_b/N₀ and BER at each individual receiver
Graphical visualization of propagating rays in the scene
Received power coverage maps
Link connectivity maps (based on minimum required SNR and BER)
Color-coded intensity plots of polarimetric electric field distributions
Incoming ray data analysis at each receiver including delay, angles of arrival and departure
Cartesian plots of path loss along defined paths
Power delay profile of the selected receiver
Polar stem charts of angles of arrival and departure of the selected receiver

Building a Propagation Scene in EM.Terrano

The Various Elements of a Propagation Scene

A typical propagation scene in EM.Terrano consists of several elements. At a minimum, you need a transmitter (Tx) at some location to launch rays into the scene and a receiver (Rx) at another location to receive and collect the incoming rays. A transmitter and a receiver together make the simplest propagation scene, representing a free-space line-of-sight (LOS) channel. In EM.Terrano, a transmitter represents a point source, while a receiver represents a point observable. Both a transmitter and a receiver are associated with point objects, which are one of the many types of geometric objects you can draw in the project workspace. Your scene might involve more than one transmitter and possibly a large grid of receivers.

A more complicated propagation scene usually contains several buildings, walls, or other kinds of scatterers and wave obstructing objects. You model all of these elements by drawing geometric objects in the project workspace or by importing external CAD models. EM.Terrano does not organize the geometric objects of your project workspace by their material composition. Rather, it groups the geometric objects into blocks based on a common type of interaction with incident rays. EM.Terrano offer the following types of object blocks:

Block/Group Type	Ray Interaction Type	Object Types Allowed	Notes
Impenetrable Surface	Ray reflection, ray diffraction	All solid & surface geometric objects, no curve objects	Basic building group for outdoor scenes
Penetrable Surface	Ray reflection, ray diffraction, ray transmission in free space	All solid & surface geometric objects, no curve objects	Behaves similar to impenetrable surface and uses thin wall approximation for generating transmitted rays, used to model hollow buildings with ray penetration, entry and exit
Terrain Surface	Ray reflection, ray diffraction	All surface geometric objects, no solid or curve objects	Behaves exactly like impenetrable surface but can change the elevation of all the buildings and transmitters and receivers located above it
Penetrable Volume	Ray reflection, ray diffraction, ray transmission and ray attenuation inside homogeneous material media	All solid geometric objects, no surface or curve objects	Used to model wave propagation inside a volumetric material block, also used for creating individual solid walls and interior building partitions and panels in indoor scenes
Base Location Set	Either ray generation or ray reception	Only point objects	Required for the definition of transmitters and receivers
Point Scatterer Set	Ray reception and ray scattering	Only point, box and sphere objects	Required for the definition of point scatterers as targets in a radar simulation
Virtual Object	No ray interaction	All types of objects	Used for representing non-physical items

Click on each type to learn more about it in the Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types.

Impenetrable surfaces, penetrable surfaces, terrain surfaces and penetrable volumes represent all the objects that obstruct the propagation of electromagnetic waves (rays) in the free space. What differentiates them is the types of physical phenomena that are used to model their interaction with the impinging rays. EM.Terrano discretizes geometric objects into a number of flat facets. The field intensity, phase and power of the reflected and transmitted rays depend on the material properties of the obstructing facet. The specular surface of a facet can be modeled locally as a simple homogeneous dielectric half-space or as a multilayer medium. In that respect, all the obstructing objects such as buildings, walls, terrain, etc. behave in a similar way:

They terminate an impinging ray and replace it with one or more new rays.
They represent a specular interface between two media of different material compositions for calculating the reflection, transmission or diffraction coefficients.

An outdoor propagation scene typically involves several buildings modeled by impenetrable surfaces. Rays hit the facets of impenetrable buildings and bounce back, but they do not penetrate the object. It is assumed that the interior of such buildings are highly dissipative due to wave absorption or diffusion. An indoor propagation scene typically involves several walls, a ceiling and a floor arranged according to a certain building layout. Penetrable surfaces are used to model the exterior and interior walls of buildings. Rays reflect off these surfaces and diffract off their edges. They also penetrate the thin surface and continue their path in the free space on the other side of the wall. Terrain surfaces with irregular shapes or possibly random rough surfaces are used as an alternative to the flat global ground. You can also build mixed scenes involving both impenetrable and penetrable blocks or irregular terrain. In the context of a propagation scene, penetrable volumes are often used to model block of rain, fog or vegetation. Base location sets are used to geometrically represent point transmitters and point receivers in the project workspace.

Sometimes it is helpful to draw graphical objects as visual clues in the project workspace. These non-physical objects must belong to a virtual object group. Virtual objects are not discretized by EM.Terrano's mesh generator, and they are not passed onto the input data files of the SBR simulation engine.

An urban propagation scene generated by EM.Terrano's "Random City" and "Basic Link" wizards. It consists of 25 cubic brick buildings, one transmitter and a large two-dimensional array of receivers.

Organizing the Propagation Scene by Block Groups

In EM.Terrano, all the geometric objects associated with the various scene elements like buildings, terrain surfaces and base location points are grouped together as blocks based on their common type. All the objects listed under a particular group in the navigation tree share the same color, texture and material properties. Once a new block group has been created in the navigation tree, it becomes the "Active" group of the project workspace, which is always displayed in bold letters. You can draw new objects under the active node. Any block group can be made active by right-clicking on its name in the navigation tree and selecting the Activate item of the contextual menu.

EM.Terrano's navigation tree.

It is recommended that you first create block groups, and then draw new objects under the active block group. However, if you start a new EM.Terrano project from scratch, and start drawing a new object without having previously defined any block groups, a new default impenetrable surface group is created and added to the navigation tree to hold your new CAD object. You can always change the properties of a block group later by accessing its property dialog from the contextual menu. You can also delete a block group with all of its objects at any time.

	You can only import external CAD models (STEP, IGES, STL, DEM, etc.) only to the CubeCAD module. You can then transfer the imported objects from CubeCAD to EM.Terrano.

Moving Objects Among Different Block Groups

You can move any geometric object or a selection of objects from one block group to another. You can also transfer objects among EM.Cube's different modules. For example, you often need to move imported CAD models of terrain or buildings from CubeCAD to EM.Terrano. To transfer objects, first select them in the project workspace or select their names in the navigation tree. Then right-click on them and select Move To → Module Name → Object Group from the contextual menu. For example, if you want to move a selected object to a block group called "Terrain_1" in EM.Terrano, then you have to select the menu item Move To → EM.Terrano → Terrain_1 as shown in the figure below. Note that you can transfer several objects altogether using the keyboards's Ctrl or Shift keys to make multiple selections.

Moving the terrain model of Mount Whitney originally imported from an external digital elevation map (DEM) file to EM.Terrano.

The imported terrain model of Mount Whitney shown in EM.Terrano's project workspace under a terrain group called "Terrain_1".

Adjustment of Block Elevation on Underlying Terrain Surfaces

In EM.Terrano, buildings and all other geometric objects are initially drawn on the XY plane. In other words, the Z-coordinates of the local coordinate system (LCS) of all blocks are set to zero until you change them. Since the global ground is located a z = 0, your buildings are seated on the ground. When your propagation scene has an irregular terrain, you would want to place your buildings on the surface of the terrain and not buried under it. This can be done automatically as part of the definition of the block group. Open the property dialog of a block group and check the box labeled Adjust Block to Terrain Elevation. All the objects belonging to that block are automatically elevated in the Z direction such that their bases sit on the surface of their underlying terrain. In effect, the LCS of each of these individual objects is translated along the global Z-axis by the amount of the Z-elevation of the terrain object at the location of the LCS.

	You have to make sure that the resolution of your terrain, its variation scale and building dimensions are all comparable. Otherwise, on a rapidly varying high-resolution terrain, you will have buildings whose bottoms touch the terrain only at a few points and parts of them hang in the air.

The property dialog of impenetrable surface showing the terrain elevation adjustment box checked.

A set of buildings on an undulating terrain without elevation adjustment.

The set of buildings on the undulating terrain after elevation adjustment.

EM.Terrano's Ray Domain & Global Environment

Why Do You Need a Finite Computational Domain?

The SBR simulation engine requires a finite computational domain for ray termination. All the stray rays that emanate from a source inside this finite domain and hit its boundaries are terminated during the simulation process. Such rays exit the computational domain and travel to the infinity, with no chance of ever reaching any receiver in the scene. When you define a propagation scene with various elements like buildings, walls, terrain, etc., a dynamic domain is automatically established and displayed as a green wireframe box that surrounds the entire scene. Every time you create a new object, the domain box is automatically adjusted and extended to enclose all the objects in the scene.

To change the ray domain settings, follow the procedure below:

Open the Ray Domain Settings Dialog by clicking the Domain button of the Simulate Toolbar, or by selecting Menu > Simulate > Computational Domain > Settings..., or by right-clicking on the Ray Domain item of the navigation tree and selecting Domain Settings... from the contextual menu, or simply using the keyboard shortcut Ctrl+A.
The size of the Ray domain is specified in terms of six Offset parameters along the ±X, ±Y and ±Z directions. The default value of all these six offset parameters is 10 project units. Change these values as you like.
You can also change the color of the domain box using the Color button.
After changing the settings, use the Apply button to make the changes effective while the dialog is still open.

EM.Terrano's domain settings dialog.

Understanding the Global Ground

Most outdoor and indoor propagation scenes include a flat ground at their bottom, which bounces incident rays back into the scene. EM.Terrano provides a global flat ground at z = 0. The global ground indeed acts as an impenetrable surface that blocks the entire computational domain from the z = 0 plane downward. It is displayed as a translucent green plane at z = 0 extending downward. The color of the ground plane is always the same as the color of the ray domain. The global ground is assumed to be made of a homogeneous dielectric material with a specified permittivity ε_r and electric conductivity σ. By default, a rocky ground is assumed with ε_r = 5 and σ = 0.005 S/m. You can remove the global ground, in which case, you will have a free space scene. To disable the global ground, open up the "Global Ground Settings" dialog, which can be accessed by right clicking on the Global Ground item in the Navigation Tree and selecting Global Ground Settings... Remove the check mark from the box labeled "Include Half-Space Ground (z<0)" to disable the global ground. This will also remove the green translucent plane from the bottom of your scene. You can also change the material properties of the global ground and set new values for the permittivity and electric conductivity of the impenetrable, half-space, dielectric medium.

Alternatively, you can use EM.Terrano's Empirical Soil Model to define the material properties of the global ground. This model requires a number of parameters: Temperature in °C, and Volumetric Water Content, Sand Content and Clay Content all as percentage.

	To model a free-space propagation scene, you have to disable EM.Terrano's default global ground.

EM.Terrano's Global Environment Settings dialog.

Defining Point Transmitters & Point Receivers for Your Propagation Scene

The Nature of Transmitters & Receivers

In EM.Terrano, transmitters and receivers are indeed point radiators used for transmitting and receiving signals at different locations of the propagation scene. From a geometric point of view, both transmitters and receivers are represented by point objects or point arrays. These are grouped as base locations in the "Physical Structure" section of the navigation tree. As radiators, transmitters and receivers are defined by a radiator type with a certain far-field radiation pattern. Consistent with EM.Cube's other computational modules, transmitters are categorizes as an excitation source, while receivers are categorized as a project observable. In other words, a transmitter is used to generate electromagnetic waves that propagate in the physical scene. A receiver, on the other hand, is used to compute the received fields and received signal power or signal-to-noise ratio (SNR). For this reason, transmitters are defined and listed under the "Sources" sections of the navigation tree, while receivers are defined and listed under the "Observables" section.

EM.Terrano provides three radiator types for point transmitter sets:

Half-wave dipole oriented along one of the three principal axes
Two collocated, orthogonally polarized, isotropic radiators
User defined (arbitrary) antenna with imported far-field radiation pattern

EM.Terrano also provides three radiator types for point receiver sets:

Half-wave dipole oriented along one of the three principal axes
Polarization-matched isotropic radiator
User defined (arbitrary) antenna with imported far-field radiation pattern

The default transmitter and receiver radiator types are both vertical (Z-directed) half-wave dipoles.

There are three different ways to define a transmitter set or a receiver set:

By defining point objects or point arrays under physical base location sets in the navigation tree and then associating them with a transmitter or receiver set
Using Python commands emag_tx, emag_rx, emag_tx_array, emag_rx_array, emag_tx_line and emag_rx_line
Using the "Basic Link" wizard

Defining a Point Transmitter Set in the Formal Way

Transmitters act as sources in a propagation scene. A transmitter is a point radiator with a fully polarimetric radiation pattern defined over the entire 3D space in the standard spherical coordinate system. EM.Terrano gives you three options for the radiator associated with a point transmitter:

Half-wave dipole
Orthogonally polarized isotropic radiators
User defined antenna pattern

By default, EM.Terrano assumes that your transmitter is a vertically polarized (Z-directed) resonant half-wave dipole antenna. This antenna has an almost omni-directional radiation pattern in all azimuth directions. It also has radiation nulls along the axis of the dipole. You can change the direction of the dipole and orient it along the X or Y axes using the provided drop-down list. The second choice of two orthogonally polarized isotropic radiators is an abstract source that is used for polarimetric channel characterization as will be discussed later.

You can override the default radiator option and select any other kind of antenna with a more complicated radiation pattern. For this purpose, you have to import a radiation pattern data file to EM.Terrano. You can model any radiating structure using EM.Cube's other computational modules, EM.Tempo, EM.Picasso, EM.Libera or EM.Illumina, and generate a 3D radiation pattern data file for it. The far-field radiation patter data are stored in a specially formatted file with a ".RAD" file extension. This file contains columns of spherical φ and θ angles as well as the real and imaginary parts of the complex-valued far-zone electric field components E_θ and E_φ. The θ- and φ-components of the far-zone electric field determine the polarization of the transmitting radiator.

	By default, EM.Terrano assumes a vertical half-wave dipole radiator for your point transmitter set.

A transmitter set always needs to be associated with an existing base location set with one or more point objects in the project workspace. Therefore, you cannot define a transmitter for your scene before drawing a point object under a base location set.

Click here to learn how to define a Point Transmitter Set.

The point transmitter set definition dialog.

Once you define a new transmitter set, its name is added in the Transmitters section of the navigation tree. The color of all the base points associated with the newly defined transmitter set changes, and an additional little ball with the transmitter color (red by default) appears at the location of each associated base point. You can open the property dialog of the transmitter set and modify a number of parameters including the Source Power in Watts and the broadcast signal Phase in degrees. The default transmitter power level is 1W or 30dBm. There is also a check box labeled Use Custom Input Power, which is checked by default. In that case, the power and phase boxes are enabled and you can change the default 1W power and 0° phase values as you wish. EM.Cube's ".RAD" radiation pattern files usually contain the value of "Total Radiated Power" in their file header. This quantity is calculated based on the particular excitation mechanism that was used to generate the pattern file in the original EM.Cube module. When the "Use Custom Input Power" check box is unchecked, EM.Terrano will use the total radiated power value of the radiation file for the SBR simulation.

	In order to modify any of the transmitter set's parameters, first you need to select the "User Defined Antenna" option, even if you want to keep the vertical half-wave dipole as your radiator.

The property dialog of a point transmitter set.

Your transmitter in EM.Teranno is indeed more sophisticated than a simple radiator. It consists of a basic "Transmitter Chain" that contains a voltage source with a series source resistance, and connected via a segment of transmission line to a transmit antenna, which is used to launch the broadcast signal into the free space. The transmitter's property dialog allows you to define the basic transmitter chain. Click the Transmitter Chain button of the Transmitter Set dialog to open the transmitter chain dialog. As shown in the figure below, you can specify the characteristics of the baseband/IF amplifier, mixer and power amplifier (PA) including stage gains and impedance mismatch factors (IMF) as well as the characteristics of the transmission line segment that connects the PA to the antenna. Note that the transmit antenna characteristics are automatically filled using the contents of the imported radiation pattern data file. The transmitter Chain dialog also calculates and reports the "Total Transmitter Chain Gain" based on your input. When you close this dialog and return to the Transmitter Set dialog, you will see the calculated value of the Effective Isotropic Radiated Power (EIRP) of your transmitter in dBm.

	If you do not modify the default parameters of the transmitter chain, a 50-Ω conjugate match condition is assumed and the power delivered to the antenna will be -3dB lower than your specified baseband power.

EM.Terrano's point transmitter chain dialog.

Defining a Point Receiver Set in the Formal Way

Receivers act as observables in a propagation scene. The objective of a SBR simulation is to calculate the far-zone electric fields and the total received power at the location of a receiver. You need to define at least one receiver in the scene before you can run a SBR simulation. Similar to a transmitter, a receiver is a point radiator, too. EM.Terrano gives you three options for the radiator associated with a point receiver set:

Half-wave dipole
Polarization matched isotropic radiator
User defined antenna pattern

By default, EM.Terrano assumes that your receiver is a vertically polarized (Z-directed) resonant half-wave dipole antenna. You can change the direction of the dipole and orient it along the X or Y axes using the provided drop-down list. An isotropic radiator has a perfect omni-directional radiation pattern in all azimuth and elevation directions. An isotropic radiator doesn't exist physically in the real world, but it can be used simply as a point in space to compute the electric field.

You may also define a complicated radiation pattern for your receiver set. In that case, you need to import a radiation pattern data file to EM.Terrano similar to the case of a transmitter set.

	By default, EM.Terrano assumes a vertical half-wave dipole radiator for your point receiver set.

Similar to transmitter sets, you define a receiver set by associating it with an existing base location set with one or more point objects in the project workspace. All the receivers belonging to the same receiver set have the same radiator type. A typical propagation scene contains one or few transmitters but usually a large number of receivers. To generate a wireless coverage map, you need to define an array of points as your base location set.

Click here to learn how to define a Point Receiver Set.

The point receiver set definition dialog.

Once you define a new receiver set, its name is added to the Receivers section of the navigation tree. The color of all the base points associated with the newly defined receiver set changes, and an additional little ball with the receiver color (yellow by default) appears at the location of each associated base point. You can open the property dialog of the receiver set and modify a number of parameters.

The property dialog of a point receiver set.

In the Receiver Set dialog, there is a drop-down list labeled Selected Element, which contains a list of all the individual receivers belonging to the receiver set. At the end of an SBR simulation, the button labeled Show Ray Data becomes enabled. Clicking this button opens the Ray Data dialog, where you can see a list of all the received rays at the selected receiver and their computed characteristics.

If you choose the "user defined antenna" option for your receiver set, it indeed consists of a basic "Receiver Chain" that contains a receive antenna connected via a segment of transmission line to the low-noise amplifier (LNA) that is terminated in a matched load. The receiver set's property dialog allows you to define the basic receiver chain. Click the Receiver Chain button of the Receiver Set dialog to open the receiver chain dialog. As shown in the figure below, you can specify the characteristics of the LNA such as its gain and noise figure in dB as well as the characteristics of the transmission line segment that connects the antenna to the LNA. Note that the receiving antenna characteristics are automatically filled from using contents of the radiation file. You have to enter values for antenna's Brightness Temperature as well as the temperature of the transmission line and the receiver's ambient temperature. The effective Receiver Bandwidth is assumed to be 100MHz, which you can change for the purpose of noise calculations. The Receive Chain dialog calculates and reports the "Noise Power" and "Total Receiver Chain Gain" based on your input. At the end of an SBR simulation, the receiver power and signal-noise ratio (SNR) of the selected receiver are calculated and they are reported in the receiver set dialog in dBm and dB, respectively. You can examine the properties of all the individual receivers and all the individual rays received by each receiver in your receiver set using the "Selected Element" drop-down list.

EM.Terrano's point receiver chain dialog.

Modulation Waveform and Detection

EM.Terrano allows you to define a digital modulation scheme for your communication link. There are currently 17 waveforms to choose from in the receiver set property dialog:

OOK
M-ary ASK
Coherent BFSK
Coherent QFSK
Coherent M-ary FSK
Non-Coherent BFSK
Non-Coherent QFSK
Non-Coherent M-ary FSK
BPSK
QPSK
Offset QPSK
M-ary PSK
DBPSK
pi/4 Gray-Coded DQPSK
M-ary QAM
MSK
GMSK (BT = 0.3)

In the above list, you need to specify the No. Levels (M) for the Mary modulation schemes, from which the No. Bits per Symbol is determined. You can also define a bandwidth for the signal, which has a default value of 100MHz. Once the SNR of the signal is found, given the specified modulation scheme, the E_b/N₀ parameter is determined, from which the bit error rate (BER) is calculated.

The Shannon – Hartley Equation estimates the channel capacity:

[math] C = B \log_2 \left( 1 + \frac{S}{N} \right) [/math]

where B in the bandwidth in Hz, and C is the channel capacity (maximum data rate) expressed in bits/s.

The spectral efficiency of the channel is defined as

[math] \eta = \log_2 \left( 1 + \frac{S}{N} \right) [/math]

The quantity E_b/N₀ is the ratio of energy per bit to noise power spectral density. It is a measure of SNR per bit and is calculated from the following equation:

[math] \frac{E_b}{N_0} = \frac{ 2^\eta - 1}{\eta} [/math]

where η is the spectral efficiency.

The relationship between the bit error rate and E_b/N₀ depends on the modulation scheme and detection type (coherent vs. non-coherent). For example, for coherent QPSK modulation, one can write:

[math] P_b = 0.5 \; \text{erfc} \left( \sqrt{ \frac{E_b}{N_0} } \right) [/math]

where P_b is the bit error rate and erfc(x) is the complementary error function:

[math] \text{erfc}(x) = 1-\text{erf}(x) = \frac{2}{\sqrt{\pi}} \int_{x}^{\infty} e^{-t^2} dt [/math]

The Minimum Required SNR parameter is used to determine link connectivity between each transmitter and receiver pair. If you check the box labeled Generate Connectivity Map in the receiver set property dialog, a binary map of the propagation scene is generated by EM.Terrano, in which one color represents a closed link and another represent no connection depending on the selected color map type of the graph. EM.Terrano also calculates the Max Permissible BER corresponding to the specified minimum required SNR and displays it in the receiver set property dialog.

A Note on EM.Terrano's Native Dipole Radiators

When you define a new transmitter set or a new receiver set, EM.Terrano assigns a vertically polarized half-wave dipole radiator to the set by default. The radiation pattern of this native dipole radiators is calculated using well-know expressions that are derived based on certain assumptions and approximations. For example, the far-zone electric field of a vertically-polarized dipole antenna can be expressed as:

[math] E_\theta(\theta,\phi) \approx j\eta_0 I_0 \frac{e^{-jk_0 r}}{2\pi r} \left[ \frac{\text{cos} \left( \frac{k_0 L}{2} \text{cos} \theta \right) - \text{cos} \left( \frac{k_0 L}{2} \right) }{\text{sin}\theta} \right] [/math]

[math] E_\phi(\theta,\phi) \approx 0 [/math]

where k₀ = 2π/λ₀ is the free-space wavenumber, λ₀ is the free-space wavelength, η₀ = 120π Ω is the free-space intrinsic impedance, I₀ is the current on the dipole, and L is the length of the dipole.

The directivity of the dipole antenna is given be the expression:

[math] D_0 \approx \frac{2}{F_1(k_0L) + F_2(k_0L) + F_3(k_0L)} \left[ \frac{\text{cos} \left( \frac{k_0 L}{2} \text{cos} \theta \right) - \text{cos} \left( \frac{k_0 L}{2} \right) }{\text{sin}\theta} \right]^2 [/math]

with

[math] F_1(x) = \gamma + \text{ln}(x) - C_i(x) [/math]

[math] F_2(x) = \frac{1}{2} \text{sin}(x) \left[ S_i(2x) - 2S_i(x) \right] [/math]

[math] F_3(x) = \frac{1}{2} \text{cos}(x) \left[ \gamma + \text{ln}(x/2) + C_i(2x) - 2C_i(x) \right] [/math]

where γ = 0.5772 is the Euler-Mascheroni constant, and C_i(x) and S_i(x) are the cosine and sine integrals, respectively:

[math] C_i(x) = - \int_{x}^{\infty} \frac{ \text{cos} \tau}{\tau} d\tau [/math]

[math] S_i(x) = \int_{0}^{x} \frac{ \text{sin} \tau}{\tau} d\tau [/math]

In the case of a half-wave dipole, L = λ₀/2, and D₀ = 1.643. Moreover, the input impedance of the dipole antenna is Z_A = 73 + j42.5 Ω. These dipole radiators are connected via 50Ω transmission lines to a 50Ω source or load. Therefore, there is always a certain level of impedance mismatch that violates the conjugate match condition for maximum power.

EM.Terrano's native half-wave dipole transmitter and receiver.

On the other hand, we you specify a user-defined antenna pattern for the transmitter or receiver sets, you import a 3D radiation pattern file that contains all the values of E_θ and E_φ for all the combinations of (θ, φ) angles. Besides the three native dipole radiators, EM.Cube also provides 3D radiation pattern files for three X-, Y- and Z-polarized half-wave resonant dipole antennas. These pattern data were generated using a full-wave solver like EM.Libera's wire MOM solver. The names of the radiation pattern files are:

DPL_STD_X.RAD
DPL_STD_Y.RAD
DPL_STD_Z.RAD

and they are located in the folder "\Documents\EMAG\Models" on your computer. Note that these are full-wave simulation data and do not involve any approximate assumptions. To use these files as an alternative to the native dipole radiators, you need to select the User Defined Antenna Pattern radio button as the the radiator type in the transmitter or receiver set property dialog.

A Note on the Rotation of Antenna Radiation Patterns

EM.Terrano's Transmitter Set dialog and Receiver Set dialog both allow you to rotate an imported radiation pattern. In that case, you need to specify the Rotation angles in degrees about the X-, Y- and Z-axes. It is important to note that these rotations are performed sequentially and in the following order: first a rotation about the X-axis, then a rotation about the Y-axis, and finally a rotation about the Z-axis. In addition, all the rotations are performed with respect to the "rotated" local coordinate systems (LCS). In other words, the first rotation with respect to the local X-axis transforms the XYZ LCS to a new primed X^′Y^′Z^′ LCS. The second rotation is performed with respect to the new Y^′-axis and transforms the X^′Y^′Z^′ LCS to a new double-primed X^′′Y^′′Z^′′ LCS. The third rotation is finally performed with respect to the new Z^′′-axis. The figures below shows single and double rotations.

The local coordinate system of a linear dipole antenna.

Rotating the dipole antenna by +90° about the local Y-axis.

Rotating the dipole antenna by +90° about the local X-axis and then by -45° by the local Y-axis.

Adjustment of Tx/Rx Elevation above a Terrain Surface

When your transmitters or receivers are located above a flat terrain like the global ground, their Z-coordinates are equal to their height above the ground, as the terrain elevation is fixed and equal to zero everywhere. In many propagation modeling problems, your transmitters and receivers may be located above an irregular terrain with varying elevation across the scene. In that case, you may want to place your transmitters or receivers at a certain height above the underlying ground. The Z-coordinate of a transmitter or receiver is now the sum of the terrain elevation at the base point and the specified height. EM.Terrano gives you the option to adjust the transmitter and receiver sets to the terrain elevation. This is done for individual transmitter sets and individual receiver sets. At the top of the Transmitter Dialog there is a check box labeled "Adjust Tx Sets to Terrain Elevation". Similarly, at the top of the Receiver Dialog there is a check box labeled "Adjust Rx Sets to Terrain Elevation". These boxes are unchecked by default. As a result, your transmitter sets or receiver sets coincide with their associated base points in the project workspace. If you check these boxes and place a transmitter set or a receiver set above an irregular terrain, the transmitters or receivers are elevated from the location of their associated base points by the amount of terrain elevation as can be seen in the figure below.

To better understand why there are two separate sets of points in the scene, note that a point array (CAD object) is used to create a uniformly spaced base set. The array object always preserves its grid topology as you move it around the scene. However, the transmitters or receivers associated with this point array object are elevated above the irregular terrain and no longer follow a strictly uniform grid. If you move the base set from its original position to a new location, the base points' topology will stay intact, while the associated transmitters or receivers will be redistributed above the terrain based on their new elevations.

A transmitter (red) and a grid of receivers (yellow) adjusted above a plateau terrain surface. The underlying base point sets (blue and orange dots) associated with the adjusted transmitters and receivers on the terrain are also visible in the figure.

Discretizing the Propagation Scene in EM.Terrano

Why Do You Need to Discretize the Scene?

EM.Terrano's SBR solver uses a method known as Geometrical Optics (GO) in conjunction with the Uniform Theory of Diffraction (UTD) to trace the rays from their originating point at the source to the individual receiver locations. Rays may hit obstructing objects on their way and get reflected, diffracted or transmitted. EM.Terrano's SBR solver can only handle diffraction off linear edges and reflection from and transmission through planar interfaces. When an incident ray hits the surface of the obstructing object, a local planar surface assumption is made at the specular point. The assumptions of linear edges and planar facets obviously work in the case of a scene with cubic buildings and a flat global ground.

In many practical scenarios, however, your buildings may have curved surfaces, or the terrain may be irregular. EM.Terrano allows you to draw any type of surface or solid geometric objects such as cylinders, cones, etc. under impenetrable and penetrable surface groups or penetrable volumes. EM.Terrano's mesh generator creates a triangular surface mesh of all the objects in your propagation scene, which is called a facet mesh. Even the walls of cubic buildings are meshed using triangular cells. This enables EM.Terrano to properly discretize composite buildings made of conjoined cubic objects.

Unlike EM.Cube's other computational modules, the density or resolution of EM.Terrano's surface mesh does not depend on the operating frequency and is not expressed in terms of the wavelength. The sole purpose of EM.Terrano's facet mesh is to discretize curved and irregular scatterers into flat facets and linear edges. Therefore, geometrical fidelity is the only criterion for the quality of a facet mesh. It is important to note that discretizing smooth objects using a triangular surface mesh typically creates a large number of small edges among the facets that are simply mesh artifacts and should not be considered as diffracting edges. For example, each rectangular face of a cubic building is subdivided into four triangles along the two diagonals. The four internal edges lying inside the face are obviously not diffracting edges. A lot of subtleties like these must be taken into account by the SBR solver to run accurate and computationally efficient simulations.

Generating the Facet Mesh

You can view and examine the discretized version of your scene's objects as they are sent to the SBR simulation engine. You can adjust the mesh resolution and increase the geometric fidelity of discretization by creating more and finer triangular facets. On the other hand, you may want to reduce the mesh complexity and send to the SBR engine only a few coarse facets to model your buildings. The resolution of EM.Terrano's facet mesh generator is controlled by the Cell Edge Length parameter, which is expressed in project length units. The default mesh cell size of 100 units might be too large for non-flat objects. You may have to set a smaller cell edge length in EM.Terrano's Mesh Settings dialog, along with a lower curvature angle tolerance value to capture the curvature of your curved structures adequately.

EM.Terrano's mesh settings dialog.

Click here to learn more about Working with Mesh Generator.

Click here to learn more about the properties of EM.Terrano's Facet Mesh Generator.

The facet mesh of the buildings in the urban propagation scene generated by EM.Terrano's Random City wizard with a cell edge length of 100m.

The facet mesh of the buildings in the urban propagation scene generated by EM.Terrano's Random City wizard with a cell edge length of 10m.

Running Ray Tracing Simulations in EM.Terrano

EM.Terrano provides a number of different simulation or solver types:

3D Field Solver
SBR Channel Analyzer
Log-Haul Channel Analyzer
Communication Link Solver
Radar Link Solver

The first three simulation types are described below. For a description of EM.Terrano's Radar Simulator, follow this link.

Running a Single-Frequency SBR Analysis

Its main solver is the 3D SBR Ray Tracer. Once you have set up your propagation scene in EM.Terrano and have defined sources/transmitters and observables/receivers for your scene, you are ready to run a SBR ray tracing simulation. You set the simulation mode in EM.Terrano's simulation run dialog. A single-frequency SBR analysis is a single-run simulation and the simplest type of ray tracing simulation in EM.Terrano. It involves the following steps:

Set the units of your project and the frequency of operation. Note that the default project unit is millimeter. Wireless propagation problems usually require meter, mile or kilometer as the project unit.
Create the blocks and draw the buildings at the desired locations.
Keep the default ray domain and accept the default global ground or change its material properties.
Define an excitation source and observables for your project.
If you intend to use transmitters and receivers in your scene, first define the required base sets and then define the transmitter and receiver sets based on them.
Run the SBR simulation engine.
Visualize the coverage map and plot other data.

You can access EM.Terrano's Simulation Run dialog by clicking the Run button of the Simulate Toolbar or by selecting Simulate → Run... or using the keyboard shortcut Ctrl+R. When you click the Run button, a new window opens up that reports the different stages of the SBR simulation and indicates the progress of each stage. After the SBR simulation is successfully completed, a message pops up and prompts the completion of the process.

EM.Terrano's simulation run dialog.

EM.Terrano's output message window.

Changing the SBR Engine Settings

There are a number of SBR simulation settings that can be accessed and changed from the Ray Tracing Engine Settings Dialog. To open this dialog, click the button labeled Settings on the right side of the Select Simulation or Solver Type drop-down list in the Run Dialog. EM.Terrano's SBR simulation engine allows you to separate the physical effects that are calculated during a ray tracing process. You can selectively enable or disable Reflection/Transmission and Edge Diffraction in the "Ray-Block Interactions" section of this dialog. By default, ray reflection and transmission and edge diffraction effects are enabled. Separating these effects sometimes help you better analyze your propagation scene and understand the impact of various blocks in the scene.

EM.Terrano allows a finite number of ray bounces for each original ray emanating from a transmitter. This is very important in situations that may involve resonance effects where rays get trapped among multiple surfaces and may bounce back and forth indefinitely. This is set using the box labeled "Max No. Ray Bounces", which has a default value of 10. Note that the maximum number of ray bounces directly affects the computation time as well as the size of output simulation data files. This can become critical for indoor propagation scenes, where most of the rays undergo a large number of reflections. Two other parameters control the diffraction computations: Max Wedge Angle in degrees and Min Edge Length in project units. The maximum wedge angle is the angle between two conjoined facets that is considered to make them almost flat or coplanar with no diffraction effect. The default value of the maximum wedge angle is 170°. The minimum edge length is size of the common edge between two conjoined facets that is considered as a mesh artifact and not a real diffracting edge. The default value of the minimum edge length is one project units.

EM.Terrano's SBR simulation engine settings dialog.

As rays travel in the scene and bounce from surfaces, they lose their power, and their amplitudes gradually diminish. From a practical point of view, only rays that have power levels above the receiver sensitivity can be effectively received. Therefore, all the rays whose power levels fall below a specified power threshold are discarded. The Ray Power Threshold is specified in dBm and has a default value of -150dBm. Keep in mind that the value of this threshold directly affects the accuracy of the simulation results as well as the size of the output data file.

You can also set the Ray Angular Resolution of the transmitter rays in degrees. By default, every transmitter emanates equi-angular ray tubes at a resolution of 1 degree. Lower angular resolutions larger than 1° speed up the SBR simulation significantly, but they may compromise the accuracy. Higher angular resolutions less than 1° increase the accuracy of the simulating results, but they also increase the computation time. The SBR Engine Settings dialog also displays the Recommended Ray Angular Resolution in degrees in a grayed-out box. This number is calculated based on the overall extents of your computational domain as well as the SBR mesh resolution. To see this value, you have to generate the SBR mesh first. Keeping the angular resolution of your project above this threshold value makes sure that the small mesh facets at very large distances from the source would not miss any impinging ray tubes during the simulation.

EM.Terrano gives a few more options for the ray tracing solution of your propagation problem. For instance, it allows you to exclude the direct line-of-sight (LOS) rays from the final solution. There is a check box for this purpose labeled "Exclude direct (LOS) rays from the solution", which is unchecked by default. EM.Terrano also allows you to superpose the received rays incoherently. In that case, the powers of individual ray are simply added to compute that total received power. This option in the check box labeled "Superpose rays incoherently" is disabled by default, too.

At the end of a ray tracing simulation, the electric field of each individual ray is computed and reported. By default, the actual received ray fields are reported, which are independent of the radiation pattern of the receive antennas. EM.Terrano provides a check box labeled "Normalize ray's E-field based on receiver pattern", which is unchecked by default. If this box is checked, the field of each ray is normalized so as to reflect that effect of the receiver antenna's radiation pattern. The received power of each ray is calculated from the following equation:

[math] P_{ray} = \frac{ | \mathbf{E_{norm}} |^2 }{2\eta_0} \frac{\lambda_0^2}{4\pi} [/math]

It can be seen that if the ray's E-field is not normalized, the computed ray power will correspond to that of a polarization matched isotropic receiver.

Polarimetric Channel Analysis

In a 3D SBR simulation, a transmitter shoots a large number of rays in all directions. The electric fields of these rays are polarimetric and their strength and polarization are determined by the designated radiation pattern of the transmit antenna. The rays travel in the propagation scene and bounce from the ground and buildings or other scatterers or get diffracted at the building edges until they reach the location of the receivers. Each individual ray has its own vectorial electric field and power. The electric fields of the received rays are then superposed coherently and polarimetrically to compute the total field at the receiver locations. The designated radiation pattern of the receivers is then used to compute the total received power by each individual receiver.

From a theoretical point of view, the radiation patterns of the transmit and receive antennas are independent of the propagation channel characteristics. For the given locations of the point transmitters and receivers, one can assume ideal isotropic radiators at these points and compute the polarimetric transfer function matrix of the propagation channel. This matrix relates the received electric field at each receiver location to the transmitted electric field at each transmitter location. In general, the vectorial electric field of each individual ray is expressed in the local standard spherical coordinate system at the transmitter and receiver locations. In other words, the polarimetric channel matrix expresses the E_θ and E_φ field components associated with each ray at the receiver location to its E_θ and E_φ field components at the transmitter location. Each ray has a delay and θ and φ angles of departure at the transmitter location and θ and φ angles of departure at the receiver location.

To perform a polarimatric channel characterization of your propagation scene, open EM.Terrano's Run Simulation dialog and select Channel Analyzer from the drop-down list labeled Select Simulation or Solver Type. At the end of the simulation, a large ray database is generated with two data files called "sbr_channel_matrix.DAT" and "sbr_ray_path.DAT". The former file contains the delay, angles of arrival and departure and complex-valued elements of the channel matrix for all the individual rays that leave each transmitter and arrive at each receiver. The latter file contains the geometric aspects of each ray such as hit point coordinates.

The "Near Real-Time" Polarimatrix Solver

After EM.Terrano's channel analyzer generates a ray database that characterizes your propagation channel polarimetrically for all the combinations of transmitter and receiver locations, a ray tracing solution of the propagation problem can readily be found in almost real time by incorporating the effects of the radiation patterns of transmit and receive antennas. This is done using the Polarimatrix Solver, which is the third option of the drop-down list labeled Select Simulation or Solver Type in EM.Terrano's Run Simulation dialog. The results of the Polarimatrix and 3D SBR solvers must be identical from a theoretical point of view. However, there might be small discrepancies between the two solutions due to roundoff errors.

Using the Polarimatrix solver can lead to a significant reduction of the total simulation time in sweep simulations that involve a large number of transmitters and receivers. Certain simulation modes of EM.Terrano are intended for the Polarimatrix solver only as will be described in the next section.

	In order to use the Polarimatrix solver, you must first generate a ray database of your propagation scene using EM.Terrano's Channel Analyzer.

EM.Terrano's Simulation Modes

EM.Terrano provides a number of different simulation modes that involve single or multiple simulation runs:

Simulation Mode	Usage	Which Solver?	Frequency	Restrictions
Single-Frequency Analysis	Simulates the propagation scene "As Is"	SBR, Channel Analyzer, Polarimatrix, Radar Simulator	Runs at the center frequency fc	None
Frequency Sweep	Varies the operating frequency of the ray tracer	SBR, Channel Analyzer, Polarimatrix, Radar Simulator	Runs at a specified set of frequency samples	None
Parametric Sweep	Varies the value(s) of one or more project variables	SBR	Runs at the center frequency fc	Requires definition of sweep variables, works only with SBR solver as the physical scene may change during the sweep
Transmitter Sweep	Activates two or more transmitters sequentially with only one transmitter broadcasting at each simulation run	Polarimatrix	Runs at the center frequency fc	Requires at least two transmitters in the scene, works only with Polarimatrix solver and requires an existing ray database
Rotational Sweep	Rotates the radiation pattern of the transmit antenna(s) sequentially to model beam steering	Polarimatrix	Runs at the center frequency fc	Works only with Polarimatrix solver and requires an existing ray database
Mobile Sweep	Considers one pair of active transmitter and receiver at each simulation run to model a mobile communication link	Polarimatrix	Runs at the center frequency fc	Requires the same number of transmitters and receivers, works only with Polarimatrix solver and requires an existing ray database

Click on each item in the above list to learn more about each simulation mode.

You set the simulation mode in EM.Terrano's simulation run dialog using the drop-down list labeled Simulation Mode. A single-frequency analysis is a single-run simulation. All the other simulation modes in the above list are considered multi-run simulations. In multi-run simulation modes, certain parameters are varied and a collection of simulation data files are generated. At the end of a sweep simulation, you can plot the output parameter results on 2D graphs or you can animate the 3D simulation data from the navigation tree.

	EM.Terrano's frequency sweep simulations are very fast because the geometrical optics (ray tracing) part of the simulation is frequency-independent.

Transmitter Sweep

When your propagation scene contains two or more transmitters, whether they all belong to the same transmitter set with the same radiation pattern or to different transmitter sets, EM.Terrano assumes all to be coherent with respect to one another. In other words, synchronous transmitters are always assumed. The rays originating from all these transmitters are superposed coherently and vectorially at each receiver. In a transmitter sweep, on the other hand, EM.Terrano assumes only one transmitter broadcasting at a time. The result of the sweep simulation is a number of received power coverage maps, each corresponding to a transmitter in the scene.

	EM.Terrano's transmitter sweep works only with the Polarimatrix Solver and requires an existing ray database previously generated using the Channel Analyzer.

Rotational Sweep

You can rotate the 3D radiation patterns of both the transmitters and receivers from the property dialog of the parent transmitter set or receiver set. This is done in advance before a SBR simulation starts. You can define one or more of the rotation angles of a transmitter set or a receiver set as sweep variables and perform a parametric sweep simulation. In that case, the entire scene and all of its buildings are discretized at each simulation run and a complete physical SBR ray tracing simulation is carried out. However, we know that the polarimetric characteristics of the propagation channel are independent of the transmitter or receiver antenna patterns or their rotation angles. A rotational sweep allows you to rotate the radiation pattern of the transmitter(s) about one of the three principal axes sequentially. This is equivalent to the steering of the beam of the transmit antenna either mechanically or electronically. The result of the sweep simulation is a number of received power coverage maps, each corresponding to one of the angular samples. To run a rotational sweep, you must specify the rotation angle.

	EM.Terrano's rotational sweep works only with the Polarimatrix Solver and requires an existing ray database previously generated using the Channel Analyzer.

Mobile Sweep

In a mobile sweep, each transmitter is paired with a receiver according to their indices in their parent sets. At each simulation run, only one (Tx, Rx) pair is considered to be active in the scene. As a result, the generated coverage map takes a different meaning implying the sequential movement of the transmitter and receiver pair along their corresponding paths. In other words, the set of point transmitters and the set of point receivers indeed represent the locations of a single transmitter and a single receiver at different instants of time. It is obvious that the total number of transmitters and total number of receivers in the scene must be equal. Otherwise, EM.Terrano will prompt an error message.

EM.Cube provides a Mobile Path Wizard that facilitates the creation of a transmitter set or a receiver set along a specified path. This path can be an existing nodal curve (polyline or NURBS curve) or an existing line objects. You can also import a sptial Cartesian data file containing the coordinates of the base location points. For more information, refer to Mobile Path Wizard.

	EM.Terrano's mobile sweep works only with the Polarimatrix Solver and requires an existing ray database previously generated using the Channel Analyzer.

Investigating Propagation Effects Selectively One at a Time

In a typical SBR ray tracing simulation, EM.Terrano includes all the propagation effects such as direct (LOS) rays, ray reflection and transmission, and edge diffractions. At the end of a SBR simulation, you can visualize the received power coverage map of your propagation scene, which appears under the receiver set item in the navigation tree. The figure below shows the received power coverage map of the random city scene with a vertically polarized half-wave dipole transmitter located 10m above the ground and a large grid of vertically polarized half-wave dipole receivers placed 1.5m above the ground. The legend box shows the limits of the color map between -23dBm as the maximum and -150dB (the default receiver sensitivity value) as the minimum.

The received power coverage map of the random city scene with a dipole transmitter.

Sometime it is helpful to change the scale of the color map to better understand the dynamic range of the coverage map. If you double-click on the legend or right-click on the coverage map's name in the navigation tree and select Properties, the Plot Settings dialog opens up. Select the User-Defined item and set the lower and upper bounds of color map as you wish.

The plot settings dialog of the coverage map.

The received power coverage map of the random city scene with a user-defined color map scale between -80dBm and -20dBm.

To better understand the various propagation effects, EM.Terrano allows you to enable or disable these effects selectively. This is done from the Ray Tracing Simulation Engine Settings dialog using the provided check boxes.

EM.Terrano's simulation run dialog showing the check boxes for controlling various propagation effects.

The received power coverage map of the random city scene with direct LOS rays only.

The received power coverage map of the random city scene with reflected rays only.

The received power coverage map of the random city scene with diffracted rays only.

Working with EM.Terrano's Simulation Data

The Ray Tracing Solvers' Output Simulation Data

Both the SBR solver and the Polarimatrix solver perform the same type of simulation but in two different ways. The SBR solver discretizes the scene including all the buildings and terrain, shoots a large number of rays from the transmitters and collects the rays at the receivers. The Polarimatrix solver does the same thing using an existing polarimetric ray database that has been previously generated using EM.Terrano's Channel Analyzer. It incorporates the effects of the radiation patterns of the transmit and receive antennas in conjunction with the polarimetric channel characteristics. At the end of a ray tracing simulation, all the polarimetric rays emanating from the transmitter(s) or other sources that are received by the individual receivers are computed, collected, sorted and saved into ASCII data files. From the ray data, the total electric field at the location of receivers as well as the total received power are computed. The individual ray data include the field components of each ray, the ray's elevation and azimuth angles of departure and arrival (departure from the transmitter location and arrival at the receiver location), and time delay of the received ray with respect to the transmitter. If you specify the temperatures, noise figure and transmission line losses in the definition of the receiver sets, the noise power level and signal-to-noise ratio (SNR) at each receiver are also calculated, and so are the E_b/N₀ and bit error rate (BER) for the selected digital modulation scheme.

Visualizing Field & Received Power Coverage Maps

In wireless propagation modeling for communication system applications, the received power at the receiver location is more important than the field distributions. In order to compute the received power, you need three pieces of information:

Total Transmitted Power (EIRP): This requires knowledge of the baseband signal power, the transmitter chain parameters, the transmission characteristics of the transmission line connecting the transmitter circuit to the transmitting antenna and the radiation characteristics of the transmitting antenna.
Channel Path Loss: This is computed through SBR simulation.
Receiver Properties: This includes the radiation characteristics of the receiving antenna, the transmission characteristics of the transmission line connecting the receiving antenna to the receiver circuit and the receiver chain parameters.

In a simple link scenario, the received power P_r in dBm is found from the following equation:

[math] P_r [dBm] = P_t [dBm] + G_{TC} + G_{TA} - PL + G_{RA} + G_{RC} [/math]

where P_t is the baseband signal power in dBm at the transmitter, G_TC and G_RC are the total transmitter and receiver chain gains in dB, respectively, G_TA and G_RA are the total transmitting and receiving antenna gains in dB, respectively, and PL is the channel path loss in dB. Keep in mind that EM.Terrano is fully polarimetric. The transmitting and receiving antenna characteristics are specified through the imported radiation pattern files, which are part of the definition of the transmitters and receivers. In particular, the polarization mismatch losses are taken into account through the polarimetric SBR ray tracing analysis.

If you specify the noise-related parameters of your receiver set, the signal-to-noise ratios (SNR) is calculated at each receiver location: SNR = P_r - P_n, where P_n is the noise power level in dB. When planning, designing and deploying a communication system between points A and B, the link is considered to be closes and a connection established if the received signal power at the location of the receiver is above the noise power level by a certain threshold. In other words, the SNR at the receiver must be greater than a certain specified minimum SNR level. You specify (SNR)_min ss part of the definition of receiver chain in the Receiver Set dialog. In the "Visualization Options" section of this dialog, you can also check the check box labeled Generate Connectivity Map. This is a binary-level black-and-white map that displays connected receivers in white and disconnected receivers in black. At the end of an SBR simulation, the computed SNR is displayed in the Receiver Set dialog for the selected receiver. The connectivity map is generated and added to the navigation tree underneath the received power coverage map node.

At the end of an SBR simulation, you can visualize the field maps and receiver power coverage map of your receiver sets. A coverage map shows the total Received Power by each of the receivers and is visualized as a color-coded intensity plot. Under each receiver set node in the navigation tree, a total of seven field maps together with a received power coverage map are added. The field maps include amplitude and phase plots for the three X, Y, Z field components plus a total electric field plot. To display a field or coverage map, simply click on its entry in the navigation tree. The 3D plot appears in the Main Window overlaid on your propagation scene. A legend box on the right shows the color scale and units (dB). The 3D coverage maps are displayed as horizontal confetti above the receivers. You can change the appearance of the receivers and maps from the property dialog of the receiver set. You can further customize the settings of the 3D field and coverage plots.

The downtown Ann Arbor propagation scene.

The electric field distribution map of the Ann Arbor scene with vertical dipole transmitter and receivers.

The received power coverage map of the Ann Arbor scene with vertical dipole transmitter and receivers.

The connectivity map of the Ann Arbor scene with SNR_min = 3dB with the basic color map option.

The connectivity map of the Ann Arbor scene with SNR_min = 20dB with the basic color map option.

Visualizing the Rays in the Scene

At the end of a SBR simulation, each receiver receives a number of rays. Some receivers may not receive any rays at all. You can visualize all the rays received by a certain receiver from the active transmitter of the scene. To do this, right click the Receivers item of the Navigation Tree. From the context menu select Show Received Rays. All the rays received by the currently selected receiver of the scene are displayed in the scene. The rays are identified by labels, are ordered by their power and have different colors for better visualization. You can display the rays for only one receiver at a time. The receiver set property dialog has a list of all the individual receivers belonging to that set. To display the rays received by another receiver, you have to change the Selected Receiver in the receiver set's property dialog. If you keep the mouse focus on this dropdown list and roll your mouse scroll wheel, you can scan the selected receivers and move the rays from one receiver to the next in the list. To remove the visualized rays from the scene, right click the Receivers item of the Navigation Tree again and from the context menu select Hide Received Rays.

You can also view the ray parameters by opening the property dialog of a receiver set. By default, the first receiver of the set is always selected. You can select any other receiver from the drop-down list labeled Selected Receiver. If you click the button labeled Show Ray Data, a new dialog opens up with a table that contains all the received rays at the selected receiver and their parameters:

Delay is the total time delay that a ray experiences travelling from the transmitter to the receiver after all the reflections, transmissions and diffractions and is expressed in nanoseconds.
Ray Field is the received electric field at the receiver location due to a specific ray and is given in dBV/m.
Ray Power is the received power at the receiver due to a specific ray and is given in dBm.
Angles of Arrival are the θ and φ angles of the incoming ray at the local spherical coordinate system of the receiver.

EM.Terrano's ray data dialog showing a selected ray.

The Ray Data Dialog also shows the Total Received Power in dBm and Total Received Field in dBV/m due to all the rays received by the receiver. You can sort the rays based on their delay, field, power, etc. To do so, simply click on the grey column label in the table to sort the rays in ascending order based on the selected parameter. You can also select any ray by clicking on its ID and highlighting its row in the table. In that case, the selected rays is highlighted in the Project Workspace and all the other rays become thin (faded).

	All the received rays are summed up coherently in a vectorial manner at the receiver location.

Visualization of received rays at the location of a selected receiver in the random city scene.

The Standard Output Data File

At the end of an SBR simulation, EM.Terrano writes a number of ASCII data files to your project folder. The main output data file is called "sbr_results.RTOUT". This file contains all the information about individual receivers and the parameters of each ray that is received by each individual receiver. At the end of an SBR simulation, the results are written into a main output data file with the reserved name of SBR_Results.RTOUT. This file has the following format:

Each receiver line has the following information:

Receiver ID
Receiver X, Y, Z coordinates
Total received power in dBm
Total number of received rays

Each rays line received by a receiver has the following information:

Ray Index
Delay in nsec
θ and φ Angles of Arrival in deg
θ and φ Angles of Departure in deg
Real and imaginary parts of the three E_x, E_y, E_z components
Number of ray hit points
Coordinates of individual hit points

The angles of arrival are the θ and φ angles of a received ray measured in degrees and are referenced in the local spherical coordinate systems centered at the location of the receiver. The angles of departure for a received ray are the θ and φ angles of the originating transmitter ray, measured in degrees and referenced in the local spherical coordinate systems centered at the location of the active transmitter, which eventually arrives at the receiver. The total time delay is measured in nanoseconds between t = 0 nsec at the time of launch from the transmitter location till being received at the receiver location.

A typical SBR output data file.

Plotting Other Simulation Results

Besides "sbr_results.out", EM.Terrano writes a number of other ASCII data files to your project folder. You can view or plot these data in EM.Cube's Data Manager. You can open data manager by clicking the Data Manager button of the Simulate Toolbar or by selecting Menu > Simulate > Data Manager from the menu bar or by right-clicking on the Data Manager item of the navigation tree and selecting Open Data Manager... from the contextual menu or by using the keyboard shortcut Ctrl+D.

The available data files in the "2D Data Files" tab of Data Manger include:

Path Loss: The channel path loss is defined as PL = P_r - EIRP. The path loss data are stored in a file called "SBR_receiver_set_name_PATHLOSS.DAT" as a function of the receiver index. The path loss data make sense only if your receiver set has the default isotropic radiator.
Power Delay Profile: The delays of the individual rays received by the selected receiver with respect to the transmitter are expressed in ns and tabulated together with the power of each ray in the file "SBR_receiver_set_name_DELAY.DAT". You can plot these data from the Data Manager as a bar chart called the power delay profile. The bars indeed correspond to the difference between the ray power in dBm and the minimum power threshold level in dBm, which makes them a positive quantity.
Angles of Arrival: These are the Theta and Phi angles of the individual rays received by the selected receiver and saved to the files "SBR_receiver_set_name_ThetaARRIVAL.ANG" and "SBR_receiver_set_name_PhiARRIVAL.ANG". You can plot them in the Data Manager in polar stem charts.

When you run a frequency or parametric sweep in EM.Terrano, a tremendous amount of data may be generated. EM.Terrano only stores the Received Power, Path Loss and SNR of the selected receiver in ASCII data files called "PREC_i.DAT", "PL_i.DAT" and "SNR_i.DAT", where is the index of the receiver set in your scene. These quantities are tabulated vs. the sweep variable's samples. You can plot these files in EM.Grid.

Click here to learn more about working with data filed and plotting graphs in EM.Cube's Data Manager.

Cartesian graph of path loss.	Bar graph of power delay profile.
Polar stem graph of Phi angle of arrival.	Polar stem graph of Theta angle of arrival.
Polar stem graph of Phi angle of departure.	Polar stem graph of Theta angle of departure.

Visualizing 3D Radiation Patterns of Transmit and Receive Antennas in the Scene

When you designate a "User Defined Antenna Pattern" as the radiator type of a transmitter set or a receiver set, EM.Terrano copies the imported radiation pattern data file from its original folder to the current project folder. The name of the ".RAD" file is listed under the 3D Data Files tab of the data manager. Sometimes it might be desired to visualize these radiation patterns in your propagation scene at the actual location of the transmitter or receiver. To do so, you have to define a new Radiation Pattern observable in the navigation tree. The label of the new observable must be identical to the name of the ".RAD" data file. In addition, the Theta and Phi angle increments of the new radiation pattern observable (expressed in degrees) must be identical to the Theta and Phi angular resolutions of the imported pattern file. If all these conditions are met, then go to the Simulate Menu and select the item Update All 3D Visualization. The contents of the 3D radiation patterns are added to the navigation tree. Click on one of the radiation pattern items in the navigation tree and it will be displayed in the scene.

The received power coverage map of the random city scene with a highly directional dipole array transmitter.

By Default, EM.Cube always visualizes the 3D radiation patterns at the origin of coordinates, i.e. at (0, 0, 0). This is because that radiation pattern data are computed in the standard spherical coordinate system centered at (0, 0, 0). The theta and phi components of the far-zone electric fields are defined with respect to the X, Y and Z axes of this system. When visualizing the 3D radiation pattern data in a propagation scene, it is more intuitive to display the pattern at the location of the transmitter or receiver. The Radiation Pattern dialog allows you to translate the pattern visualization to any arbitrary point in the project workspace. It also allows you to scale up or scale down the pattern visualization with respect to the background scene.

In the example shown above, the imported pattern data file is called "Dipole_Array1.RAD". Therefore, the label of the radiation pattern observable is chosen to be "Dipole_Array1". The theta and phi angle increments are both 1° in this case. The radiation pattern has been elevated by 10m to be positioned at the location of the transmitter and a scaling factor of 0.3 has been used.

Setting the pattern parameters in the radiation pattern dialog.

Visualization of the 3D radiation pattern of the directional transmitter in the random city scene.

There is an important catch to remember here. When you define a radiation pattern observable for your project, EM.Terrano will attempt to compute the overall effective radiation pattern of the entire physical structure. However, in this case, you defined the radiation pattern observable merely for visualization purposes. To stop EM.Terrano from computing the actual radiation pattern of your entire scene, there is a check box in EM.Terrano's Ray Tracer Simulation Engine Settings dialog that is labeled Do not compute new radiation patterns. This box is checked by default, which means the actual radiation pattern of your entire scene will not be computed automatically. But you need to remember to uncheck this box if you ever need to compute a new radiation pattern using EM.Terrano's SBR solver as an asymptotic EM solver (see next section).

EM.Terrano's Run Simulation dialog.

Using EM.Terrano as an Asymptotic Field Solver

Like every other electromagnetic solver, EM.Terrano's SBR ray tracer requires an excitation source and one or more observables for the generation of simulation data. EM.Terrano offers several types of sources and observables for a SBR simulation. You already learned about the transmitter set as a source and the receiver set as an observable. You can mix and match different source types and observable types depending on the requirements of your modeling problem.

The available source types in EM.Terrano are:

Source Type	Applications	Restrictions
Point Transmitter Set	Modeling realsitic antennas & link budget calculations	Requires to be associated with a base location point set
Hertzian Short Dipole	Almost omni-directional physical radiator	None, stand-alone source
Huygens Source	Used for modeling equivalent sources imported from other EM.Cube modules	None, stand-alone source imported from a Huygens surface data file

Click on each type to learn more about it in the Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types.

The available observables types in EM.Terrano are:

Source Type	Applications	Restrictions
Point Receiver Set	Generating received power coverage maps & link budget calculations	Requires to be associated with a base location point set
Distributed Receiver Set	Computing received power at a receiver characterized by Huygens surface data	None, stand-alone source imported from a Huygens surface data file
Near-Field Sensor	Generating electric and magnetic field distribution maps	None, stand-alone observable
Far-Field Radiation Pattern	Computing the effective radiation pattern of a radiator in the presence of a large scattering scene	None, stand-alone observable
Huygens Surface	Collecting tangential field data on a box to be used later as a Huygens source in other EM.Cube modules	None, stand-alone observable

Click on each type to learn more about it in the Glossary of EM.Cube's Simulation Observables & Graph Types.

When you define a far-field observable in EM.Terrano, a collection of invisible, isotropic receivers are placed on the surface of a large sphere that encircles your propagation scene and all of its geometric objects. These receivers are placed uniformly on the spherical surface at a spacing that is determined by your specified angular resolutions. In most cases, you need to define angular resolutions of at least 1° or smaller. Note that this is different than the transmitter rays' angular resolution. You may have a large number of transmitted rays but not enough receivers to compute the effective radiation pattern at all azimuth and elevation angles. Also keep in mind that with 1° Theta and Phi angle increments, you will have a total of 181 × 361 = 65,341 spherically placed receivers in your scene.

	Computing radiation patterns using EM.Terrano's SBR solver typically takes much longer computation times than using EM.Cube's other computational modules.

Computed 3D radiation pattern of two vertical short dipole radiators placed 1m apart in the free space at 1GHz.

Statistical Analysis of Propagation Scene

EM.Terrano's coverage maps display the received power at the location of all the receivers. The receivers together from a set/ensemble, which might be uniformly spaced or distributed across the propagation scene or may consist of randomly scattered radiators. Every coverage map shows the Mean and Standard Deviation of the received power for all the receivers involved. These information are displayed at the bottom of the coverage map's legend box and are expressed in dB.

When you run either a frequency sweep or a parametric sweep simulation in EM.Terrano, you have the option to generate two additional coverage maps: one for the mean of all the individual sample coverage maps and another for their standard deviation. To do so, in the Run Dialog, check the box labeled "Create Mean and Standard Deviation received power coverage maps". Note that the mean and standard deviation values displayed on the individual coverage maps correspond to the spatial statistics of the receivers in the scene, while the mean and standard deviation coverage maps show the statistics with respect to the frequency or other sweep variable sets at each point in the site. Also, note that both of the mean and standard deviation coverage maps have their own spatial mean and standard deviation values expressed in dB at the bottom of their legend box.

EM.Terrano's simulation run dialog showing frequency sweep as the simulation mode along with statistical analysis.

The mean coverage map at the end of a frequency sweep.

The standard deviation coverage map at the end of a frequency sweep.

Back to the Top of the Page

EM.Terrano Tutorial Gateway

Back to EM.Cube Main Page

@@ Line 1: / Line 1: @@
-<!-- Taking out this picture for now for consistency
+[[Image:Splash-prop.jpg|right|720px]]
-[[File:urban.png]]-->
+<strong><font color="#4e1985" size="4">True 3D, Coherent, Polarimetric Ray Tracer That Simulates Very Large Urban Scenes In Just Few Minutes!</font></strong>
-EM.Terrano is a physics-based, site-specific, wave propagation modeling tool that enables engineers to quickly determine how radio waves propagate in urban, natural or mixed environments. The rapid growth of wireless communications along with the high costs associated with the design and deployment of effective wireless infrastructures underline a persistent need for computer aided communication network planning tools. Wireless engineers have long used simplistic statistical prediction models based on measurements that often exhibit considerable errors especially in areas having mixed building sizes.
+<table>
+<tr>
+<td>[[image:Cube-icon.png | link=Getting_Started_with_EM.Cube]] [[image:cad-ico.png | link=Building_Geometrical_Constructions_in_CubeCAD]] [[image:fdtd-ico.png | link=EM.Tempo]] [[image:static-ico.png | link=EM.Ferma]] [[image:planar-ico.png | link=EM.Picasso]] [[image:metal-ico.png | link=EM.Libera]]  [[image:po-ico.png | link=EM.Illumina]]</td>
+<tr>
+</table>
+[[Image:Tutorial_icon.png|30px]] '''[[EM.Cube#EM.Terrano_Documentation | EM.Terrano Tutorial Gateway]]'''
-Since its introduction in 2002, EM.Terrano has helped wireless engineers around the globe model the physical channel and the mechanisms by which radio signals propagate from transmitters to receivers. EM.Terrano’s advanced ray tracing simulator finds the dominant propagation paths specific to the site in question. It calculates the true signal characteristics at the actual locations using physical databases of the buildings and terrain at a given site, not those of a statistically average or representative environment. EM.Terrano’s ray tracer is based on the shoot-and-bounce-rays (SBR) method, which utilizes geometrical optics (GO) in combination with uniform theory of diffraction (UTD) models of building edges.
+[[Image:Back_icon.png|30px]] '''[[EM.Cube | Back to EM.Cube Main Page]]'''
+==Product Overview==
-The new EM.Terrano 2013 has been totally reconstructed based on our integrated EM.Cube software foundation. This integration has created the opportunity to inject a host of new powerful features such as a highly customizable terrain generator, DEM terrain import, complex building constructions, and versatile interior wall arrangements for indoor propagation modeling. As a result of this seamless interface with EM.Cube's other modules, you can now model complex antenna systems in [[EM.Picasso]], [[EM.Tempo]] or [[EM.Libera]], and generate antenna radiation patterns than can be used to model directional transmitters and receivers at the two ends of your propagation channel. Conversely, you can analyze a propagation scene in EM.Terrano and import the rays received at a certain receiver location as coherent plane wave sources to [[EM.Picasso]], [[EM.Tempo]] or [[EM.Libera]]. You can also model periodic wall or ground structures using the periodic simulation capability of [[EM.Picasso]] or [[EM.Tempo]] and generate macromodels for their reflection and transmission coefficients as functions of the ray incidence angles. You can then define buildings or terrains in your propagation scene that are governed by such macromodels.
+===EM.Terrano in a Nutshell ===
-== A Wireless Propagation Primer ==
+EM.Terrano is a physics-based, site-specific, wave propagation modeling tool that enables engineers to quickly determine how radio waves propagate in urban, natural or mixed environments. EM.Terrano's simulation engine is equipped with a fully polarimetric, coherent 3D ray tracing solver based on the Shooting-and-Bouncing-Rays (SBR) method, which utilizes geometrical optics (GO) in combination with uniform theory of diffraction (UTD) models of building edges. EM.Terrano lets you analyze and resolve all the rays transmitted from one ore more signal sources, which propagate in a real physical channel made up of buildings, terrain and other obstructing structures. EM.Terrano finds all the rays received by a receiver at a particular location in the physical site and computes their vectorial field and power levels, time delays, angles of arrival and departure, etc. Using EM.Terrano you can examine the connectivity of a communication link between any two points in a real specific propagation site.
-Every wireless communication system involves a transmitter that transmits some sort of signal (voice, video, data, etc.), a receiver that receives and detects the transmitted signal, and a channel in which the signal is transmitted into the air and travels from the location of the transmitter to the location of the receiver. The channel is the physical medium in which the electromagnetic waves propagate. The successful design of a communication system depends on an accurate link budget analysis that determines whether the receiver receives adequate signal power to detect it against the background noise. The simplest channel is the free space. Real communication channels, however, are more complicated and involve a large number of wave scatterers. For example, in an urban environment, the obstructing buildings, vehicles and vegetation reflect, diffract or attenuate the propagating radio waves. As a result, the receiver receives a distorted signal that contains several components with different power levels and different time delays arriving from different angles.
-The different rays arriving at a receiver location create constructive and destructive interference patterns. This is known as the multipath effect. This together with the shadowing effects caused by building obstructions lead to channel fading. In many wireless applications, the total received power by the receiver is all that matters. In some others, the angle of arrival of the rays as well as their polarization are of immense interest. A fully polarimetric, coherent ray tracer like EM.Cube's Shooting-and-Bouncing-Rays (SBR) solver lets you compute and resolve all the rays received by a receiver including their power levels, time delays and angles of arrival.
+Since its introduction in 2002, EM.Terrano has helped wireless engineers around the globe model the physical channel and the mechanisms by which radio signals propagate in various environments. EM.Terrano’s advanced ray tracing simulator finds the dominant propagation paths at each specific physical site. It calculates the true signal characteristics at the actual locations using physical databases of the buildings and terrain at a given site, not those of a statistically average or representative environment. The earlier versions of EM.Terrano's SBR solver relied on certain assumptions and approximations such as the vertical plane launch (VPL) method or 2.5D analysis of urban canyons with prismatic buildings using two separate vertical and horizontal polarizations. In 2014, we introduced a new fully 3D polarimetric SBR solver that accurately traces all the three X, Y and Z components of the electric fields (both amplitude and phase) at every point inside the computational domain. Using a 3D CAD modeler, you can now set up any number of buildings with arbitrary geometries, no longer limited to vertical prismatic shapes. Versatile interior wall arrangements allow indoor propagation modeling inside complex building configurations. The most significant recent development is a multicore parallelized SBR simulation engine that takes advantage of ultrafast k-d tree algorithms borrowed from the field of computer graphics and video gaming to achieve the ultimate speed and efficiency in geometrical optics ray tracing.
-=== Free Space Propagation Channel ===
+[[Image:Info_icon.png|30px]] Click here to learn more about the '''[[Basic Principles of SBR Ray Tracing | Basic SBR Theory]]'''.
-In a free-space line-of-sight (LOS) communication system, the signal propagates directly from the transmitter to the receiver without encountering any obstacles (scatterers). Electromagnetic waves propagate in the form of spherical waves with a functional dependence of e<sup>j(&omega;</sup><sup>t-k<sub>0</sub>R)</sup>/R, where R is the distance between the transmitter and receiver, <math>\omega = 2\pi f</math>, f is the signal frequency, <math>k_0 = \tfrac{\omega}{c} = \tfrac{2\pi}{\lambda}</math>, c is the speed of light, and &lambda;<sub>0</sub> is the free-space wavelength at the operational frequency. By the time the signal arrives at the location of the receiver, it undergoes two changes. It is attenuated and its power drops by a factor of 1/R<sup>2</sup>, and additionally, it experiences a phase shift of <math>\tfrac{2\pi R}{\lambda_0}</math>, which is equivalent to a time delay of R/c. The signal attenuation from the transmitter to the receiver is usually quantified by '''Path Loss''' defined as the ratio of the received signal power (P<sub>R</sub>) to the transmitted signal power (P<sub>T</sub>). Assuming isotropic transmitting and receiving radiators (i.e. radiating uniformly in all directions), the Path Loss in a free-space line-of-sight communication system is given by Friis’ formula:
+<table>
+<tr>
+<td>
+[[Image:Manhattan1.png|thumb|left|420px|A large urban propagation scene featuring lower Manhattan.]]
+</td>
+</tr>
+</table>
-:<math> \frac{P_R}{P_T} = \left( \frac{\lambda_0}{4\pi R} \right)^2 </math>
+=== EM.Terrano as the Propagation Module of EM.Cube ===
-<!--[[File:friis1.png]]-->
-The above formula assumes that the receiving antenna is polarization-matched. Normally, there is a polarization mismatch between the transmitting and receiving antennas. In the case of directional transmitting and receiving antennas, Friis’ formula takes the following form:
+EM.Terrano is the ray tracing '''Propagation Module''' of '''[[EM.Cube]]''', a comprehensive, integrated, modular electromagnetic modeling environment. EM.Terrano shares the visual interface, 3D parametric CAD modeler, data visualization tools, and many more utilities and features collectively known as [[Building_Geometrical_Constructions_in_CubeCAD | CubeCAD]] with all of [[EM.Cube]]'s other computational modules.
-:<math> \frac{P_R}{P_T} = G_T G_R \left( \frac{\lambda_0}{4\pi R} \right)^2 ( \mathbf{ \hat{u}_T \cdot \hat{u}_R } )</math>
+With the seamless integration of EM.Terrano with [[EM.Cube]]'s other modules, you can now model complex antenna systems in [[EM.Tempo]], [[EM.Libera]], [[EM.Picasso]] or [[EM.Illumina]], and generate antenna radiation patterns that can be used to model directional transmitters and receivers at the two ends of your propagation channel. Conversely, you can analyze a propagation scene in EM.Terrano, collect all the rays received at a certain receiver location and import them as coherent plane wave sources to [[EM.Tempo]], [[EM.Libera]], [[EM.Picasso]] or [[EM.Illumina]].
-<!--[[File:friis2.png]]-->
-where '''u<sub>T</sub>''' and '''u<sub>R</sub>''' are the unit polarization vectors of the transmitting and receiving antennas, and G<sub>T</sub> and G<sub>R</sub> are their gains, respectively.
+[[Image:Info_icon.png|30px]] Click here to learn more about '''[[Getting_Started_with_EM.Cube | EM.Cube Modeling Environment]]'''.
-[[File:los.png]]
+=== Advantages & Limitations of EM.Terrano's SBR Solver ===
-Figure: A Line-of-Sight (LOS) Propagation Scenario.
+EM.Terrano's SBR simulation engine utilizes an intelligent ray tracing algorithm that is based on the concept of k-dimensional trees. A k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are particularly useful for searches that involve multidimensional search keys such as range searches and nearest neighbor searches. In a typical large radio propagation scene, there might be a large number of rays emanating from the transmitter that may never hit any obstacles. For example, upward-looking rays in an urban propagation scene quickly exit the computational domain. Rays that hit obstacles on their path, on the other hand, generate new reflected and transmitted rays. The k-d tree algorithm traces all these rays systematically in a very fast and efficient manner. Another major advantage of k-d trees is the fast processing of multi-transmitters scenes.
-=== Multipath Propagation Channel ===
+EM.Terrano performs fully polarimetric and coherent SBR simulations with arbitrary transmitter antenna patterns. Its SBR simulation engine is a true asymptotic &quot;field&quot; solver. The amplitudes and phases of all the three vectorial field components are computed, analyzed and preserved throughout the entire ray tracing process from the source location to the field observation points. You can visualize the magnitude and phase of all six electric and magnetic field components at any point in the computational domain. In most scenes, the buildings and the ground or terrain can be assumed to be made of homogeneous materials. These are represented by their electrical properties such as permittivity &epsilon;<sub>r</sub> and electric conductivity &sigma;. More complex scenes may involve a multilayer ground or multilayer building walls. In such cases, one can no longer use the simple reflection or transmission coefficient formulas for homogeneous medium interfaces. EM.Terrano calculates the reflection and transmission coefficients of multilayer structures as functions of incident angle, frequency and polarization and uses them at the respective specular points.
-Free-space line-of-sight communications is an ideal scenario that is typically used to model aerial or space applications. In ground-based systems, the presence of the ground as a very large reflecting surface affects the signal propagation to a large extent. Along the path from a transmitter to a receiver, the signal may also encounter many obstacles and scatterers such as buildings, vegetation, etc. In an urban canyon environment with many buildings of different heights and other scatterers, a line of sight between the transmitter and receiver can hardly be established. In such cases, the propagating signals bounce back and forth among the building surfaces. It is these reflected or diffracted signals that are often received and detected by the receiver. Such environments are referred to as “multipath”. The group of rays arriving at a specific receiver location experience different attenuations and different time delays. This gives rise to constructive and destructive interference patterns that cause fast fading. As a receiver moves locally, the receiver power level fluctuates sizably due to these fading effects.
+It is very important to keep in mind that SBR is an asymptotic electromagnetic analysis technique that is based on Geometrical Optics (GO) and the Uniform Theory of Diffraction (UTD). It is not a &quot;full-wave&quot; technique, and it does not provide a direct numerical solution of Maxwell's equations. SBR makes a number of assumptions, chief among them, a very high operational frequency such that the length scales involved are much larger than the operating wavelength. Under this assumed regime, electromagnetic waves start to behave like optical rays. Virtually all the calculations in SBR are based on far field approximations. In order to maintain a high computational speed for urban propagation problems, EM.Terrano ignores double diffractions. Diffractions from edges give rise to a large number of new secondary rays. The power of diffracted rays drops much faster than reflected rays. In other words, an edge-diffracted ray does not diffract again from another edge in EM.Terrano. However, reflected and penetrated rays do get diffracted from edges just as rays emanated directly from the sources do.
-The use of statistical models for prediction of fading effects is widely popular among communication system designers. These models are either based on measurement data or derived from simplistic analytical frameworks. The statistical models often exhibit considerable errors especially in areas having mixed building sizes. In such cases, one needs to perform a physics-based, site-specific analysis of the propagation environment to accurately identify and establish all the possible signal paths from the transmitter to the receiver. This involves an electromagnetic analysis of the scene with all of its geometrical and physical details.
+<table>
+<tr>
+<td>
+[[Image:Multipath_Rays.png|thumb|left|500px|A multipath urban propagation scene showing all the rays collected by a receiver.]]
+</td>
+</tr>
+</table>
-Link budget analysis for a multipath channel is a challenging task due to the large size of the computational domains involved. Typical propagation scenes usually involve length scales on the order of thousands of wavelengths. To calculate the path loss between the transmitter and receiver, one must solve Maxwell's equations in an extremely large space. Full-wave numerical techniques like the Finite Difference Time Domain (FDTD) method, which require a fine discretization of the computational domain, are therefore impractical for solving large-scale propagation problems. The practical solution is to use asymptotic techniques such as SBR, which utilize analytical techniques over large distances rather than a brute force discretization of the entire computational domain. Such asymptotic techniques, of course, have to compromise modeling accuracy for practical computation feasibility.
+== EM.Terrano Features at a Glance ==
-[[File:multi1_tn.png]]
+=== Scene Definition / Construction ===
-Figure 1: A multipath propagation scene showing all the rays arriving at a particular receiver.
+<ul>
+	<li>
+		Buildings/blocks with arbitrary geometries and material properties</li>
+	<li>
+		Buildings/blocks with impenetrable surfaces or penetrable surfaces using thin wall approximation</li>
+	<li>
+		Multilayer walls for indoor propagation scenes</li>
+	<li>
+		Penetrable volume blocks with arbitrary geometries and material properties</li>
+	<li>
+		Import of shapefiles and STEP, IGES and STL CAD model files for scene construction</li>
+	<li>
+		Terrain surfaces with arbitrary geometries and material properties and random rough surface profiles</li>
+	<li>
+		Import of digital elevation map (DEM) terrain models</li>
+	<li>
+		Python-based random city wizard with randomized building locations, extents and orientations</li>
+	<li>
+		Python-based wizards for generation of parameterized multi-story office buildings and several terrain scene types</li>
+	<li>
+		Standard half-wave dipole transmitters and receivers oriented along the principal axes</li>
+	<li>
+		Short Hertzian dipole sources with arbitrary orientation</li>
+	<li>
+		Isotropic receivers or receiver grids for wireless coverage modeling</li>
+	<li>
+		Radiator sets with 3D directional antenna patterns (imported from other modules or external files)</li>
+	<li>
+		Full three-axis rotation of imported antenna patterns</li>
+	<li>
+		Interchangeable radiator-based definition of transmitters and receivers (networks of transceivers)</li>
+</ul>
-=== The SBR Method ===
+=== Wave Propagation Modeling ===
-EM.Cube's [[Propagation Module]] provides an asymptotic ray tracing simulation engine that is based on a technique known as Shooting-and-Bouncing-Rays (SBR). In this technique, propagating spherical waves are modeled as ray tubes or beams that emanate from a source, travel in space, bounce from obstacles and are collected by the receiver. As rays propagate away from their source (transmitter), they begin to spread (or diverge) over distance. In other words, the cross section or footprint of a ray tube expands as a function of the distance from the source. EM.Cube uses an accurate equi-angular ray generation scheme to that produces almost identical ray tubes in all directions to satisfy energy and power conservation requirements.
+<ul>
+	<li>
+		Fully 3D polarimetric and coherent Shoot-and-Bounce-Rays (SBR) simulation engine</li>
+	<li>
+		GTD/UTD diffraction models for diffraction from building edges and terrain</li>
+	<li>
+		Triangular surface mesh generator for discretization of arbitrary block geometries</li>
+	<li>
+		Super-fast geometrical/optical ray tracing using advanced k-d tree algorithms</li>
+	<li>
+		Intelligent ray tracing with user defined angular extents and resolution</li>
+	<li>
+		Ray reflection, edge diffraction and ray transmission through multilayer walls and material volumes</li>
+	<li>
+		Communication link analysis for superheterodyne transmitters and receivers</li>
+	<li>
+digital modulation waveforms for the calculation of E<sub>b</sub>/N<sub>0</sub> and Bit error rate (BER)</li>
+	<li>
+		Incredibly fast frequency sweeps of the entire propagation scene in a single SBR simulation run</li>
+	<li>
+		Parametric sweeps of scene elements like building properties, or radiator heights and rotation angles</li>
+	<li>
+		Statistical analysis of the propagation scene</li>
+	<li>
+		Polarimetric channel characterization for MIMO analysis</li>
+	<li>
+		"Almost real-time" Polarimatrix solver using an existing ray database</li>
+	<li>
+		"Almost real-time" transmitter sweep using the Polarimatrix solver</li>
+	<li>
+		"Almost real-time" rotational sweep for modeling beam steering using the Polarimatrix solver</li>
+	<li>
+		"Almost real-time" mobile sweep for modeling mobile communications between Tx-Rx pairs along a mobile path using the Polarimatrix solver</li>
+</ul>
-When a ray hits an obstructing surface, one or more of the following phenomena may happen:
+=== Data Generation &amp; Visualization ===
-# Reflection from the locally flat surface
+<ul>
-# Transmission through the locally flat surface
+	<li>
-# Diffraction from an edge between two conjoined locally flat surfaces
+		Standard output parameters for received power, path loss, SNR, E<sub>b</sub>/N<sub>0</sub> and BER at each individual receiver</li>
+	<li>
+		Graphical visualization of propagating rays in the scene</li>
+	<li>
+		Received power coverage maps</li>
+	<li>
+		Link connectivity maps (based on minimum required SNR and BER)</li>
+	<li>
+		Color-coded intensity plots of polarimetric electric field distributions</li>
+	<li>
+		Incoming ray data analysis at each receiver including delay, angles of arrival and departure</li>
+	<li>
+		Cartesian plots of path loss along defined paths</li>
+	<li>
+		Power delay profile of the selected receiver</li>
+	<li>
+		Polar stem charts of angles of arrival and departure of the selected receiver</li>
+</ul>
-EM.Cube discretizes all the objects of the scene into flat triangular facets. Obviously, rectangular and cubic objects preserve their geometric shapes through this discretization. Objects with curved surfaces such as cylinders, cones or spheres, are approximated by &quot;polymesh&quot; representations. The geometric fidelity of the resulting mesh depends on the specified mesh edge length. When a ray hits a triangular facet, the propagating spherical wave is approximated as a plane wave at the specular point. The reflection and transmission coefficients of the surface are calculated at the operational frequency and at the particular ray incident angle.
+== Building a Propagation Scene in EM.Terrano ==
-A new reflected ray is generated at the specular point, which starts traveling and bouncing around in the scene. If the obstructing surface is penetrable, a second transmitted ray is generated and added to the scene. If the ray hits the edge of an obstacle, it is diffracted from that edge. This leads to the creation of a cone of new rays, which greatly complicate the computational problem. The Uniform Theory of Diffraction (UTD) is used to calculate the wedge diffraction coefficients at the edges of scattering blocks. Note that reflection, transmission and diffraction coefficients are all dependent on the polarization of the incident plane wave.
+=== The Various Elements of a Propagation Scene ===
-A receiver may receive a large number of rays: direct line-of-sight rays from the transmitter, rays reflected or diffracted off the ground or terrain, rays reflected or diffracted from buildings or rays transmitted through buildings. Each received ray is characterized by its power, delay and angles of arrival, which are the spherical coordinate angles &theta; and &phi; of the incoming ray. The actual signal received and detected by the receiver is the superposition of all these rays with different power levels and different time delays. Most of the time, you will be interested in the coverage map of an area, which shows how much power is received by a grid of receivers spread over the area from a given fixed transmitter.
+A typical propagation scene in EM.Terrano consists of several elements. At a minimum, you need a transmitter (Tx) at some location to launch rays into the scene and a receiver (Rx) at another location to receive and collect the incoming rays. A transmitter and a receiver together make the simplest propagation scene, representing a free-space line-of-sight (LOS) channel. In EM.Terrano, a transmitter represents a point source, while a receiver represents a point observable. Both a transmitter and a receiver are associated with point objects, which are one of the many types of geometric objects you can draw in the project workspace. Your scene might involve more than one transmitter and possibly a large grid of receivers.
-=== Ray Reflection & Transmission ===
+A more complicated propagation scene usually contains several buildings, walls, or other kinds of scatterers and wave obstructing objects. You model all of these elements by drawing geometric objects in the project workspace or by importing external CAD models. EM.Terrano does not organize the geometric objects of your project workspace by their material composition. Rather, it groups the geometric objects into blocks based on a common type of interaction with incident rays. EM.Terrano offer the following types of object blocks:
-[[File:reflect.png|thumb|350px|The Incident, Reflected and Transmitted Rays at the Interface Between Two Dielectric Media]]
+{| class="wikitable"
+|-
+! scope="col"| Icon
+! scope="col"| Block/Group Type
+! scope="col"| Ray Interaction Type
+! scope="col"| Object Types Allowed
+! scope="col"| Notes
+|-
+| style="width:30px;" | [[File:impenet_group_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Impenetrable Surface | Impenetrable Surface]]
+| style="width:200px;" | Ray reflection, ray diffraction
+| style="width:250px;" | All solid & surface geometric objects, no curve objects
+| style="width:300px;" | Basic building group for outdoor scenes
+|-
+| style="width:30px;" | [[File:penet_surf_group_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Penetrable Surface | Penetrable Surface]]
+| style="width:200px;" | Ray reflection, ray diffraction, ray transmission in free space
+| style="width:250px;" | All solid & surface geometric objects, no curve objects
+| style="width:300px;" | Behaves similar to impenetrable surface and uses thin wall approximation for generating transmitted rays, used to model hollow buildings with ray penetration, entry and exit
+|-
+| style="width:30px;" | [[File:terrain_group_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Terrain Surface | Terrain Surface]]
+| style="width:200px;" | Ray reflection, ray diffraction
+| style="width:250px;" | All surface geometric objects, no solid or curve objects
+| style="width:300px;" | Behaves exactly like impenetrable surface but can change the elevation of all the buildings and transmitters and receivers located above it
+|-
+| style="width:30px;" | [[File:penet_vol_group_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Penetrable Volume | Penetrable Volume]]
+| style="width:200px;" | Ray reflection, ray diffraction, ray transmission and ray attenuation inside homogeneous material media
+| style="width:250px;" | All solid geometric objects, no surface or curve objects
+| style="width:300px;" | Used to model wave propagation inside a volumetric material block, also used for creating individual solid walls and interior building partitions and panels in indoor scenes
+|-
+| style="width:30px;" | [[File:base_group_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Base Location Set | Base Location Set]]
+| style="width:200px;" | Either ray generation or ray reception
+| style="width:250px;" | Only point objects
+| style="width:300px;" | Required for the definition of transmitters and receivers
+|-
+| style="width:30px;" | [[File:scatterer_group_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Point Scatterer Set | Point Scatterer Set]]
+| style="width:200px;" | Ray reception and ray scattering
+| style="width:250px;" | Only point, box and sphere objects
+| style="width:300px;" | Required for the definition of point scatterers as targets in a radar simulation
+|-
+| style="width:30px;" | [[File:Virt_group_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Virtual_Object_Group | Virtual Object]]
+| style="width:200px;" | No ray interaction
+| style="width:250px;" | All types of objects
+| style="width:300px;" | Used for representing non-physical items
+|}
-The incident, reflected and transmitted rays are each characterized by a triplet of unit vectors:
+Click on each type to learn more about it in the [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types]].
-* <math>( \mathbf{ \hat{u}_{\|}, \hat{u}_{\perp}, \hat{k} } )</math> representing the incident parallel polarization vector, incident perpendicular polarization vector and incident propagation vector, respectively.
+Impenetrable surfaces, penetrable surfaces, terrain surfaces and penetrable volumes represent all the objects that obstruct the propagation of electromagnetic waves (rays) in the free space. What differentiates them is the types of physical phenomena that are used to model their interaction with the impinging rays. EM.Terrano discretizes geometric objects into a number of flat facets. The field intensity, phase and power of the reflected and transmitted rays depend on the material properties of the obstructing facet. The specular surface of a facet can be modeled locally as a simple homogeneous dielectric half-space or as a multilayer medium. In that respect, all the obstructing objects such as buildings, walls, terrain, etc. behave in a similar way:
-* <math>( \mathbf{ \hat{u}_{\|}', \hat{u}_{\perp}', \hat{k}' } )</math> representing the reflected parallel polarization vector, reflected perpendicular polarization vector and reflected propagation vector, respectively.
-* <math>( \mathbf{ \hat{u}_{\|}'', \hat{u}_{\perp}'', \hat{k}'' } )</math> representing the transmitted parallel polarization vector, transmitted perpendicular polarization vector and transmitted propagation vector, respectively.
-The reflected ray is assumed to originate from a virtual image source point. The three triplets constitute three orthonormal basis systems. Below, it is assumed that the two dielectric media have permittivities &epsilon;<sub>1</sub> and &epsilon;<sub>2</sub>, and permeabilities &mu;<sub>1</sub> and &mu;<sub>2</sub>, respectively. A lossy medium with a conductivity &sigma; can be modeled by a complex permittivity &epsilon;<sub>r</sub> = &epsilon;'<sub>r</sub> –j&sigma;/&epsilon;<sub>0</sub>. Assuming '''n''' to be the unit normal to the interface plane between the two media, and Z<sub>0</sub> = 120&Omega; , the incident polarization vectors as well as all the reflected and transmitted vectors are found as:
+* They terminate an impinging ray and replace it with one or more new rays.
+* They represent a specular interface between two media of different material compositions for calculating the reflection, transmission or diffraction coefficients.
-:<math> \mathbf{ \hat{u}_{\perp} = \frac{\hat{k} \times \hat{n}}{|\hat{k} \times \hat{n}|} } </math>
+An outdoor propagation scene typically involves several buildings modeled by impenetrable surfaces. Rays hit the facets of impenetrable buildings and bounce back, but they do not penetrate the object. It is assumed that the interior of such buildings are highly dissipative due to wave absorption or diffusion. An indoor propagation scene typically involves several walls, a ceiling and a floor arranged according to a certain building layout. Penetrable surfaces are used to model the exterior and interior walls of buildings. Rays reflect off these surfaces and diffract off their edges. They also penetrate the thin surface and continue their path in the free space on the other side of the wall. Terrain surfaces with irregular shapes or possibly random rough surfaces are used as an alternative to the flat global ground. You can also build mixed scenes involving both impenetrable and penetrable blocks or irregular terrain. In the context of a propagation scene, penetrable volumes are often used to model block of rain, fog or vegetation. Base location sets are used to geometrically represent point transmitters and point receivers in the project workspace.
-:<math> \mathbf{ \hat{u}_{\|} = \hat{u}_{\perp} \times \hat{k} } </math>
+Sometimes it is helpful to draw graphical objects as visual clues in the project workspace. These non-physical objects must belong to a virtual object group. Virtual objects are not discretized by EM.Terrano's mesh generator, and they are not passed onto the input data files of the SBR simulation engine.
-<!--[[File:frml1.png]]-->
-The reflected unit vectors are found as:
+<table>
+<tr>
+<td>
+[[Image:PROP MAN2.png|thumb|left|720px|An urban propagation scene generated by EM.Terrano's "Random City" and "Basic Link" wizards. It consists of 25 cubic brick buildings, one transmitter and a large two-dimensional array of receivers. ]]
+</td>
+</tr>
+</table>
-:<math> \mathbf{ \hat{k}' = \hat{k} - 2(\hat{k} \cdot \hat{n}) \hat{n} } </math>
+=== Organizing the Propagation Scene by Block Groups ===
-:<math> \mathbf{ \hat{u}_{\perp}' = \hat{u}_{\perp} } </math>
+In EM.Terrano, all the geometric objects associated with the various scene elements like buildings, terrain surfaces and base location points are grouped together as blocks based on their common type. All the objects listed under a particular group in the navigation tree share the same color, texture and material properties. Once a new block group has been created in the navigation tree, it becomes the "Active" group of the project workspace, which is always displayed in bold letters. You can draw new objects under the active node. Any block group can be made active by right-clicking on its name in the navigation tree and selecting the '''Activate''' item of the contextual menu.
-:<math> \mathbf{ \hat{u}_{\|}' = \hat{u}_{\perp}' \times \hat{k}' } </math>
+<table>
-<!--[[File:frml2.png]]-->
+<tr>
+<td>
+[[Image:PROP MAN1.png|thumb|left|480px|EM.Terrano's navigation tree.]]
+</td>
+</tr>
+</table>
-The transmitted unit vectors are found as:
+It is recommended that you first create block groups, and then draw new objects under the active block group. However, if you start a new EM.Terrano project from scratch, and start drawing a new object without having previously defined any block groups, a new default impenetrable surface group is created and added to the navigation tree to hold your new CAD object. You can always change the properties of a block group later by accessing its property dialog from the contextual menu. You can also delete a block group with all of its objects at any time.
-:<math> \mathbf{ \hat{k}'' = \hat{n} \times a - \sqrt{1-a \cdot a} \; \hat{n} } </math>
+{{Note|You can only import external CAD models (STEP, IGES, STL, DEM, etc.) only to the CubeCAD module. You can then transfer the imported objects from CubeCAD to EM.Terrano.}}
-:<math> \mathbf{ \hat{u}_{\perp}'' = \hat{u}_{\perp} } </math>
-:<math> \mathbf{ \hat{u}_{\|}'' = \hat{u}_{\perp}'' \times \hat{k}'' } </math>
+=== Moving Objects Among Different Block Groups ===
-<!--[[File:frml3.png]]-->
-where
+You can move any geometric object or a selection of objects from one block group to another. You can also transfer objects among [[EM.Cube]]'s different modules. For example, you often need to move imported CAD models of terrain or buildings from CubeCAD to EM.Terrano. To transfer objects, first select them in the project workspace or select their names in the navigation tree. Then right-click on them and select <b>Move To &rarr; Module Name &rarr; Object Group</b> from the contextual menu. For example, if you want to move a selected object to a block group called "Terrain_1" in EM.Terrano, then you have to select the menu item '''Move To &rarr; EM.Terrano &rarr; Terrain_1''' as shown in the figure below. Note that you can transfer several objects altogether using the keyboards's {{key|Ctrl}} or {{key|Shift}} keys to make multiple selections.
-:<math> \mathbf{a} = (k_1/k_2) \mathbf{\hat{k} \times \hat{n}}</math>
+<table>
+<tr>
+<td>
+[[Image:PROP MAN3.png|thumb|left|720px|Moving the terrain model of Mount Whitney originally imported from an external digital elevation map (DEM) file to EM.Terrano.]]
+</td>
+</tr>
+<tr>
+<td>
+[[Image:PROP MAN4.png|thumb|left|720px|The imported terrain model of Mount Whitney shown in EM.Terrano's project workspace under a terrain group called "Terrain_1".]]
+</td>
+</tr>
+</table>
-:<math> k_1 = k_0 \sqrt{\varepsilon_1 \mu_1} </math>
+=== Adjustment of Block Elevation on Underlying Terrain Surfaces ===
-:<math> k_2 = k_0 \sqrt{\varepsilon_2 \mu_2} </math>
+In EM.Terrano, buildings and all other geometric objects are initially drawn on the XY plane. In other words, the Z-coordinates of the local coordinate system (LCS) of all blocks are set to zero until you change them. Since the global ground is located a z = 0, your buildings are seated on the ground. When your propagation scene has an irregular terrain, you would want to place your buildings on the surface of the terrain and not buried under it. This can be done automatically as part of the definition of the block group. Open the property dialog of a block group and check the box labeled '''Adjust Block to Terrain Elevation'''. All the objects belonging to that block are automatically elevated in the Z direction such that their bases sit on the surface of their underlying terrain. In effect, the LCS of each of these individual objects is translated along the global Z-axis by the amount of the Z-elevation of the terrain object at the location of the LCS.
-:<math> \eta_1 = Z_0 \sqrt{\mu_1 / \varepsilon_1} </math>
+{{Note| You have to make sure that the resolution of your terrain, its variation scale and building dimensions are all comparable. Otherwise, on a rapidly varying high-resolution terrain, you will have buildings whose bottoms touch the terrain only at a few points and parts of them hang in the air.}}
-:<math> \eta_2 = Z_0 \sqrt{\mu_2 / \varepsilon_2} </math>
+<table>
+<tr>
+<td>
+[[Image:PROP MAN5.png|thumb|left|480px|The property dialog of impenetrable surface showing the terrain elevation adjustment box checked.]]
+</td>
+</tr>
+</table>
+<table>
+<tr>
+<td>
+[[Image:PROP MAN6.png|thumb|left|360px|A set of buildings on an undulating terrain without elevation adjustment.]]
+</td>
+<td>
+[[Image:PROP MAN7.png|thumb|left|360px|The set of buildings on the undulating terrain after elevation adjustment.]]
+</td>
+</tr>
+</table>
-:<math> \sin\theta'' = \frac{k_1}{k_2}\sin\theta \text{ if } \sin\theta \le k_2/k_1</math>
+== EM.Terrano's Ray Domain & Global Environment ==
-<!--
-[[File:frml4.png]]
-[[File:frml5.png]]
+=== Why Do You Need a Finite Computational Domain? ===
--->
-The reflection coefficients at the interface are calculated for the two parallel and perpendicular polarizations as:
+The SBR simulation engine requires a finite computational domain for ray termination. All the stray rays that emanate from a source inside this finite domain and hit its boundaries are terminated during the simulation process. Such rays exit the computational domain and travel to the infinity, with no chance of ever reaching any receiver in the scene. When you define a propagation scene with various elements like buildings, walls, terrain, etc., a dynamic domain is automatically established and displayed as a green wireframe box that surrounds the entire scene. Every time you create a new object, the domain box is automatically adjusted and extended to enclose all the objects in the scene.
-:<math>
+To change the ray domain settings, follow the procedure below:
-R_{\|} = \frac
-{ \eta_2(\mathbf{ \hat{k}'' \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) }
-{ \eta_2(\mathbf{ \hat{k}'' \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) }
-= \frac{\eta_2 \cos\theta'' - \eta_1 \cos\theta} {\eta_2 \cos\theta'' + \eta_1 \cos\theta}
+* Open the Ray Domain Settings Dialog by clicking the '''Domain''' [[File:image025.jpg]] button of the '''Simulate Toolbar''', or by selecting '''Menu > Simulate > Computational Domain > Settings...''', or by right-clicking on the '''Ray Domain''' item of the navigation tree and selecting '''Domain Settings...''' from the contextual menu, or simply using the keyboard shortcut {{key|Ctrl+A}}.
+* The size of the Ray domain is specified in terms of six '''Offset''' parameters along the ±X, ±Y and ±Z directions. The default value of all these six offset parameters is 10 project units. Change these values as you like.
+* You can also change the color of the domain box using the {{key|Color}} button.
+* After changing the settings, use the {{key|Apply}} button to make the changes effective while the dialog is still open.
-= \frac{Z_{2\|} - Z_{1\|}} {Z_{2\|} + Z_{1\|}}
+<table>
-</math>
+<tr>
+<td>
+[[Image:PROP15.png|thumb|left|480px|EM.Terrano's domain settings dialog.]]
+</td>
+</tr>
+</table>
+=== Understanding the Global Ground ===
-:<math>
+Most outdoor and indoor propagation scenes include a flat ground at their bottom, which bounces incident rays back into the scene. EM.Terrano provides a global flat ground at z = 0. The global ground indeed acts as an impenetrable surface that blocks the entire computational domain from the z = 0 plane downward. It is displayed as a translucent green plane at z = 0 extending downward. The color of the ground plane is always the same as the color of the ray domain. The global ground is assumed to be made of a homogeneous dielectric material with a specified permittivity &epsilon;<sub>r</sub> and electric conductivity &sigma;. By default, a rocky ground is assumed with &epsilon;<sub>r</sub> = 5 and &sigma; = 0.005 S/m. You can remove the global ground, in which case, you will have a free space scene. To disable the global ground, open up the "Global Ground Settings" dialog, which can be accessed by right clicking on the '''Global Ground''' item in the Navigation Tree and selecting '''Global Ground Settings... '''Remove the check mark from the box labeled '''&quot;Include Half-Space Ground (z&lt;0)&quot;''' to disable the global ground. This will also remove the green translucent plane from the bottom of your scene. You can also change the material properties of the global ground and set new values for the permittivity and electric conductivity of the impenetrable, half-space, dielectric medium.
-R_{\perp} = \frac
-{ \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k}'' \cdot \hat{n} }) }
-{ \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k}'' \cdot \hat{n} }) }
-= \frac{\eta_2 / \cos\theta'' - \eta_1 / \cos\theta} {\eta_2 / \cos\theta'' + \eta_1 / \cos\theta}
+Alternatively, you can use EM.Terrano's '''Empirical Soil Model''' to define the material properties of the global ground. This model requires a number of parameters: Temperature in &deg;C, and Volumetric Water Content, Sand Content and Clay Content all as percentage.
-= \frac{Z_{2\perp} - Z_{1\perp}} {Z_{2\perp} + Z_{1\perp}}
+{{Note|To model a free-space propagation scene, you have to disable EM.Terrano's default global ground.}}
-</math>
-<!--[[File:frml6.png]]-->
-=== Penetration Through Thin Walls Or Surfaces ===
+<table>
+<tr>
+<td>
+[[Image:Global environ.png|thumb|left|720px|EM.Terrano's Global Environment Settings dialog.]]
+</td>
+</tr>
+</table>
-In &quot;Thin Wall Approximation&quot;, we assume that an incident ray gives rise to two rays, one is reflected at the specular point, and the other is transmitted almost in the same direction as the incident ray. The reflected ray is assumed to originate from a virtual image source point. Similar to the case of reflection and transmission at the interface between two dielectric media, here too we have three triplets of unit vectors, which all form orthonormal basis systems.
+== Defining Point Transmitters &amp; Point Receivers for Your Propagation Scene ==
-[[File:thinwalltrans.png]]
+=== The Nature of Transmitters & Receivers ===
-The Incident and Transmitted Rays through a Thin Wall
+In EM.Terrano, transmitters and receivers are indeed point radiators used for transmitting and receiving signals at different locations of the propagation scene. From a geometric point of view, both transmitters and receivers are represented by point objects or point arrays. These are grouped as base locations in the "Physical Structure" section of the navigation tree. As radiators, transmitters and receivers are defined by a radiator type with a certain far-field radiation pattern. Consistent with [[EM.Cube]]'s other computational modules, transmitters are categorizes as an excitation source, while receivers are categorized as a project observable. In other words, a transmitter is used to generate electromagnetic waves that propagate in the physical scene. A receiver, on the other hand, is used to compute the received fields and received signal power or signal-to-noise ratio (SNR). For this reason, transmitters are defined and listed under the "Sources" sections of the navigation tree, while receivers are defined and listed under the "Observables" section.
-The transmission coefficients are calculated for the two parallel and perpendicular polarizations as:
+EM.Terrano provides three radiator types for point transmitter sets:
-:<math>
+#Half-wave dipole oriented along one of the three principal axes
-T_{\|} = \frac{(1-{\Gamma_{\|}}^2) \exp(-jk_2 d (\mathbf{ \hat{k}'' \cdot \hat{n}}))}
+#Two collocated, orthogonally polarized, isotropic radiators
-{ 1-{\Gamma_{\|}}^2 \exp( -2jk_2 d (\mathbf{ \hat{k}'' \cdot \hat{n} }) ) }
+#User defined (arbitrary) antenna with imported far-field radiation pattern
-</math>
+EM.Terrano also provides three radiator types for point receiver sets:
-:<math>
+#Half-wave dipole oriented along one of the three principal axes
-T_{\perp} = \frac{(1-{\Gamma_{\perp}}^2) \exp(-jk_2 d (\mathbf{ \hat{k}'' \cdot \hat{n}}))}
+#Polarization-matched isotropic radiator
-{ 1-{\Gamma_{\perp}}^2 \exp( -2jk_2 d (\mathbf{ \hat{k}'' \cdot \hat{n} }) ) }
+#User defined (arbitrary) antenna with imported far-field radiation pattern
-</math>
-<!--[[File:frml20.png]]-->
-where
+The default transmitter and receiver radiator types are both vertical (Z-directed) half-wave dipoles.
-:<math>
+There are three different ways to define a transmitter set or a receiver set:
-\Gamma_{\|} = \frac
-{ \eta_2(\mathbf{ \hat{k}'' \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) }
-{ \eta_2(\mathbf{ \hat{k}'' \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) }
-= \frac{\eta_2 \cos\theta'' - \eta_1 \cos\theta} {\eta_2 \cos\theta'' + \eta_1 \cos\theta}
+*By defining point objects or point arrays under physical base location sets in the navigation tree and then associating them with a transmitter or receiver set
+*Using Python commands emag_tx, emag_rx, emag_tx_array, emag_rx_array, emag_tx_line and emag_rx_line
+*Using the "Basic Link" wizard
-= \frac{Z_{2\|} - Z_{1\|}} {Z_{2\|} + Z_{1\|}}
+=== Defining a Point Transmitter Set in the Formal Way ===
-</math>
+Transmitters act as sources in a propagation scene. A transmitter is a point radiator with a fully polarimetric radiation pattern defined over the entire 3D space in the standard spherical coordinate system. EM.Terrano gives you three options for the radiator associated with a point transmitter:
-:<math>
+* Half-wave dipole
-\Gamma_{\perp} = \frac
+* Orthogonally polarized isotropic radiators
-{ \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k}'' \cdot \hat{n} }) }
+* User defined antenna pattern
-{ \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k}'' \cdot \hat{n} }) }
-= \frac{\eta_2 / \cos\theta'' - \eta_1 / \cos\theta} {\eta_2 / \cos\theta'' + \eta_1 / \cos\theta}
+By default, EM.Terrano assumes that your transmitter is a vertically polarized (Z-directed) resonant half-wave dipole antenna. This antenna has an almost omni-directional radiation pattern in all azimuth directions. It also has radiation nulls along the axis of the dipole. You can change the direction of the dipole and orient it along the X or Y axes using the provided drop-down list. The second choice of two orthogonally polarized isotropic radiators is an abstract source that is used for polarimetric channel characterization as will be discussed later.
-= \frac{Z_{2\perp} - Z_{1\perp}} {Z_{2\perp} + Z_{1\perp}}
+You can override the default radiator option and select any other kind of antenna with a more complicated radiation pattern. For this purpose, you have to import a radiation pattern data file to EM.Terrano. You can model any radiating structure using [[EM.Cube]]'s other computational modules, [[EM.Tempo]], [[EM.Picasso]], [[EM.Libera]] or [[EM.Illumina]], and generate a 3D radiation pattern data file for it. The far-field radiation patter data are stored in a specially formatted file with a &quot;'''.RAD'''&quot; file extension. This file contains columns of spherical &phi; and &theta; angles as well as the real and imaginary parts of the complex-valued far-zone electric field components '''E<sub>&theta;</sub>''' and '''E<sub>&phi;</sub>'''. The &theta;- and &phi;-components of the far-zone electric field determine the polarization of the transmitting radiator.
-</math>
-<!--[[File:frml21.png]]-->
-=== Wedge Diffraction From Edges ===
+{{Note|By default, EM.Terrano assumes a vertical half-wave dipole radiator for your point transmitter set.}}
-For the purpose of calculation of diffraction from building edges, we define a &quot;Wedge&quot; as having two faces, the 0-face and the ''n''-face. The wedge angle is a = (2-''n'')p, where the parameter ''n'' is required for the calculation of diffraction coefficients. All the diffracted rays lie on a cone with its vertex at the diffraction point and a wedge angle equal to the angle of incidence in the opposite direction. A diffracted ray is assumed to originate from a virtual image source point. Three triplets of unit vectors are defined as follows:
+A transmitter set always needs to be associated with an existing base location set with one or more point objects in the project workspace. Therefore, you cannot define a transmitter for your scene before drawing a point object under a base location set.
-* <math>\mathbf{(\hat{u}_0, \hat{u}_l, \hat{t})}</math> representing the unit vector normal to the edge and lying in the plane of the 0-face, the unit vector normal to the 0-face, and the unit vector along the edge, respectively.
+[[Image:Info_icon.png|40px]] Click here to learn how to define a '''[[Glossary_of_EM.Cube%27s_Materials,_Sources,_Devices_%26_Other_Physical_Object_Types#Point_Transmitter_Set | Point Transmitter Set]]'''.
-* <math>\mathbf{(\hat{u}_f, \hat{u}_b, \hat{t})}</math> representing the incident forward polarization vector, incident backward polarization vector and incident propagation vector, respectively.
-* <math>\mathbf{(\hat{u}_f', \hat{u}_b', \hat{t}')}</math> representing the diffracted forward polarization vector, diffracted backward polarization vector and diffracted propagation vector, respectively.
-The three triplets constitute three orthonormal basis systems. The propagation vector '''k'''' of the diffracted ray has to be constructed based on the diffraction cone as follows:
+<table>
+<tr>
+<td> [[Image:Terrano L1 Fig11.png|thumb|left|480px|The point transmitter set definition dialog.]] </td>
+</tr>
+</table>
-:<math> \mathbf{\hat{k}'} = \cos\phi_w \mathbf{\hat{u}_0} + \sin\phi_w \mathbf{\hat{u}_l} +
+Once you define a new transmitter set, its name is added in the '''Transmitters''' section of the navigation tree. The color of all the base points associated with the newly defined transmitter set changes, and an additional little ball with the transmitter color (red by default) appears at the location of each associated base point. You can open the property dialog of the transmitter set and modify a number of parameters including the '''Source Power''' in Watts and the broadcast signal '''Phase''' in degrees. The default transmitter power level is 1W or 30dBm. There is also a check box labeled '''Use Custom Input Power''', which is checked by default. In that case, the power and phase boxes are enabled and you can change the default 1W power and 0&deg; phase values as you wish. [[EM.Cube]]'s ".RAD" radiation pattern files usually contain the value of &quot;Total Radiated Power&quot; in their file header. This quantity is calculated based on the particular excitation mechanism that was used to generate the pattern file in the original [[EM.Cube]] module. When the "Use Custom Input Power" check box is unchecked, EM.Terrano will use the total radiated power value of the radiation file for the SBR simulation.
-\mathbf{(\hat{k} \cdot \hat{t}) \hat{t}}, \quad 0 \le \phi_w \le \alpha</math>
-<!--[[File:frml8.png]]-->
-where the resolution of the angle &theta;<sub>w</sub> is chosen to be the same as the resolution of the incident ray.
+{{Note|In order to modify any of the transmitter set's parameters, first you need to select the "User Defined Antenna" option, even if you want to keep the vertical half-wave dipole as your radiator.}}
-[[File:diffract.png]]
+<table>
+<tr>
+<td>
+[[File:NewTxProp.png|thumb|left|720px|The property dialog of a point transmitter set.]]
+</td>
+</tr>
+</table>
-Figure: The Incident Ray and Diffract Ray Cone at the Edge of a Building
+Your transmitter in EM.Teranno is indeed more sophisticated than a simple radiator. It consists of a basic "Transmitter Chain" that contains a voltage source with a series source resistance, and connected via a segment of transmission line to a transmit antenna, which is used to launch the broadcast signal into the free space. The transmitter's property dialog allows you to define the basic transmitter chain. Click the {{key|Transmitter Chain}} button of the Transmitter Set dialog to open the transmitter chain dialog. As shown in the figure below, you can specify the characteristics of the baseband/IF amplifier, mixer and power amplifier (PA) including stage gains and impedance mismatch factors (IMF) as well as the characteristics of the transmission line segment that connects the PA to the antenna. Note that the transmit antenna characteristics are automatically filled using the contents of the imported radiation pattern data file. The transmitter Chain dialog also calculates and reports the "Total Transmitter Chain Gain" based on your input. When you close this dialog and return to the Transmitter Set dialog, you will see the calculated value of the Effective Isotropic Radiated Power (EIRP) of your transmitter in dBm.
-The other unit vectors for the incident and diffracted rays are found as:
+{{Note| If you do not modify the default parameters of the transmitter chain, a 50-&Omega; conjugate match condition is assumed and the power delivered to the antenna will be -3dB lower than your specified baseband power.}}
+<table>
+<tr>
+<td> [[File:NewTxChain.png|thumb|left|720px|EM.Terrano's point transmitter chain dialog.]] </td>
+</tr>
+</table>
-:<math> \mathbf{ \hat{u}_f = \frac{\hat{k} \times \hat{t}}{|\hat{k} \times \hat{t}|} } </math>
+=== Defining a Point Receiver Set in the Formal Way ===
-:<math> \mathbf{ \hat{u}_b = \hat{k} \times \hat{u}_f } </math>
+Receivers act as observables in a propagation scene. The objective of a SBR simulation is to calculate the far-zone electric fields and the total received power at the location of a receiver. You need to define at least one receiver in the scene before you can run a SBR simulation. Similar to a transmitter, a receiver is a point radiator, too. EM.Terrano gives you three options for the radiator associated with a point receiver set:
-:<math> \mathbf{ \hat{u}_f' = \frac{\hat{k}' \times \hat{t}}{|\hat{k}' \times \hat{t}|} } </math>
+* Half-wave dipole
+* Polarization matched isotropic radiator
+* User defined antenna pattern
-:<math> \mathbf{ \hat{u}_b' = \hat{k}' \times \hat{u}_f' } </math>
+By default, EM.Terrano assumes that your receiver is a vertically polarized (Z-directed) resonant half-wave dipole antenna. You can change the direction of the dipole and orient it along the X or Y axes using the provided drop-down list. An isotropic radiator has a perfect omni-directional radiation pattern in all azimuth and elevation directions. An isotropic radiator doesn't exist physically in the real world, but it can be used simply as a point in space to compute the electric field.
-<!--[[File:frml9.png]]-->
-The diffraction coefficients are calculated in the following way:
+You may also define a complicated radiation pattern for your receiver set. In that case, you need to import a radiation pattern data file to EM.Terrano similar to the case of a transmitter set.
-[[File:frml11.png]]
+{{Note|By default, EM.Terrano assumes a vertical half-wave dipole radiator for your point receiver set.}}
-where ''F(x)'' is the Fresnel Transition function:
+Similar to transmitter sets, you define a receiver set by associating it with an existing base location set with one or more point objects in the project workspace. All the receivers belonging to the same receiver set have the same radiator type. A typical propagation scene contains one or few transmitters but usually a large number of receivers. To generate a wireless coverage map, you need to define an array of points as your base location set.
-:<math> F(x) = 2j \sqrt{x} e^{jx} \int_{\sqrt{x}}^{\infty} e^{-j\tau^2} \, d\tau </math>
+[[Image:Info_icon.png|40px]] Click here to learn how to define a '''[[Glossary_of_EM.Cube%27s_Simulation_Observables_%26_Graph_Types#Point_Receiver_Set | Point Receiver Set]]'''.
-<!--[[File:frml12.png]]-->
-In the above equations, we have
+<table>
+<tr>
+<td> [[Image:Terrano L1 Fig12.png|thumb|left|480px|The point receiver set definition dialog.]] </td>
+</tr>
+</table>
-:<math>
+Once you define a new receiver set, its name is added to the '''Receivers''' section of the navigation tree. The color of all the base points associated with the newly defined receiver set changes, and an additional little ball with the receiver color (yellow by default) appears at the location of each associated base point. You can open the property dialog of the receiver set and modify a number of parameters.
-\begin{align}
-s = |\rho_D - \rho_S| \\
-s' = |\rho_D - \rho_r|
-\end{align}
-</math>
-:<math>L = \frac{s s' \sin^2 \beta'}{s + s'} </math>
+<table>
+<tr>
+<td>
+[[File:NewRxProp.png|thumb|left|720px|The property dialog of a point receiver set.]]
+</td>
+</tr>
+</table>
-:<math>a^{\pm}(\nu) = 2\cos^2 \left( \frac{2n\pi N^{\pm} - \nu}{2} \right), \quad \nu = \phi \pm \phi' </math>
+In the Receiver Set dialog, there is a drop-down list labeled '''Selected Element''', which contains a list of all the individual receivers belonging to the receiver set. At the end of an SBR simulation, the button labeled {{key|Show Ray Data}} becomes enabled. Clicking this button opens the Ray Data dialog, where you can see a list of all the received rays at the selected receiver and their computed characteristics.
-<!--
+If you choose the "user defined antenna" option for your receiver set, it indeed consists of a basic "Receiver Chain" that contains a receive antenna connected via a segment of transmission line to the low-noise amplifier (LNA) that is terminated in a matched load. The receiver set's property dialog allows you to define the basic receiver chain. Click the {{key|Receiver Chain}} button of the Receiver Set dialog to open the receiver chain dialog. As shown in the figure below, you can specify the characteristics of the LNA such as its gain and noise figure in dB as well as the characteristics of the transmission line segment that connects the antenna to the LNA. Note that the receiving antenna characteristics are automatically filled from using contents of the radiation file. You have to enter values for antenna's '''Brightness Temperature''' as well as the temperature of the transmission line and the receiver's ambient temperature. The effective '''Receiver Bandwidth''' is assumed to be 100MHz, which you can change for the purpose of noise calculations. The Receive Chain dialog calculates and reports the "Noise Power" and "Total Receiver Chain Gain" based on your input. At the end of an SBR simulation, the receiver power and signal-noise ratio (SNR) of the selected receiver are calculated and they are reported in the receiver set dialog in dBm and dB, respectively. You can examine the properties of all the individual receivers and all the individual rays received by each receiver in your receiver set using the "Selected Element" drop-down list.
-[[File:frml10.png]]
-[[File:frml13.png]]
+<table>
--->
+<tr>
+<td> [[File:NewRxChain.png|thumb|left|720px|EM.Terrano's point receiver chain dialog.]] </td>
+</tr>
+</table>
-where <math>N^{\pm}</math> are the integers which most closely satisfy the equations <math> 2n\pi N^{\pm} - \nu = \pm \pi </math>.
+=== Modulation Waveform and Detection ===
-=== SBR As An Asymptotic EM Solver ===
+EM.Terrano allows you to define a digital modulation scheme for your communication link. There are currently 17 waveforms to choose from in the receiver set property dialog:
-EM.Cube's SBR simulation engine can be used as a versatile and powerful asymptotic electromagnetic (EM) solver. If you compare EM.Cube's [[Propagation Module]] with its other computational modules, you will notice a lot of similarities. While other modules group objects primarily by their material properties, [[Propagation Module]] categorizes the types of obstructing surfaces. Besides sharing the same ray-surface interaction mechanisms, all the objects belonging to a surface group also share the same material properties. [[Propagation Module]] offers similar source types and similar observable types as the other computational modules. For instance, the Hertzian dipole sources used in a SBR simulation are identical to those offered in PO, MoM3D and Planar modules. The plane wave sources are identical across all computational modules. [[Propagation Module]]'s sensor field planes, far field observables (either radiation patterns or RCS) and Huygens surfaces are all fully compatible with EM.Cube's other computational modules.
+*OOK
+*M-ary ASK
+*Coherent BFSK
+*Coherent QFSK
+*Coherent M-ary FSK
+*Non-Coherent BFSK
+*Non-Coherent QFSK
+*Non-Coherent M-ary FSK
+*BPSK
+*QPSK
+*Offset QPSK
+*M-ary PSK
+*DBPSK
+*pi/4 Gray-Coded DQPSK
+*M-ary QAM
+*MSK
+*GMSK (BT = 0.3)
-As an asymptotic EM solver, the SBR engine can be used to model large-scale electromagnetic radiation and scattering problems. An example of this kind is radiation of simple or complex antennas in the presence of large scattering platforms. You have to keep in mind that by using an asymptotic technique in place of a full-wave method, you trade computational speed and lower memory requirements for modeling accuracy. In particular, the SBR method cannot take into account the electromagnetic coupling effects among nearby radiators or scatterers. However, when your scene spans thousands of wavelengths, an SBR simulation might often prove to be your sole practical solution.
+In the above list, you need to specify the '''No. Levels (M)''' for the Mary modulation schemes, from which the '''No. Bits per Symbol''' is determined. You can also define a bandwidth for the signal, which has a default value of 100MHz. Once the SNR of the signal is found, given the specified modulation scheme, the E<sub>b</sub>/N<sub>0</sub> parameter is determined, from which the bit error rate (BER) is calculated.
-=== Novelties Of EM.Cube's SBR Solver ===
+The Shannon – Hartley Equation estimates the channel capacity:
-EM.Cube's new SBR simulation engine utilizes an intelligent ray tracing algorithm based on the concept of  k-dimensional trees. A k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. k-d trees are particularly useful for searches that involve multidimensional search keys such as range searches and nearest neighbor searches. In a typical large radio propagation scene, there might be a large number of rays emanating from the transmitter that may never hit any obstacles. For example, upward-looking rays in an urban propagation scene quickly exit the computational domain. Rays that hit obstacles on their path, on the other hand, generate new reflected and transmitted rays. The k-d tree algorithm traces all these rays systematically in a very fast and efficient manner. Another major advantage of k-d trees is the fast processing of multi-transmitters scenes. Unlike the previous versions of the SBR solver which could handle one transmitter at a time and would superpose all the resulting rays at the end of the simulation, the new SBR shoots rays from all the transmitters at the same time.
+<math> C = B \log_2 \left( 1 + \frac{S}{N} \right)  </math>
-EM.Cube's new SBR simulation engine performs fully polarimetric and coherent SBR simulations with arbitrary transmitter antenna patterns. The new engine solves directly for the vectorial field components at the receiver locations or field observation points. This is far more rigorous than the previous versions of the SBR solver which primarily utilized ray power calculations based on the two vertical and horizontal polarizations. In other words, EM.Cube's new SBR engine is a truly asymptotic &quot;field&quot; solver. As a result, you can visualize the magnitude and phase of all six electric and magnetic field components at any point in the computational domain. For power calculations at the receiver location, an isotropic, polarization-matched, receiving antenna is assumed.
+where B in the bandwidth in Hz, and C is the channel capacity (maximum data rate) expressed in bits/s.
-In most scenes, the buildings and the ground or terrain can be assumed to be made of homogeneous materials. These are represented by their electrical properties such as permittivity e and electric conductivity s. More complex scenes may involve a multilayer ground or multilayer building walls. In such cases, one can no longer use the simple reflection or transmission coefficient formulas for homogeneous medium interfaces. EM.Cube calculates the reflection and transmission coefficients of multilayer structures as functions of incident angle, frequency and polarization and uses them at the respective specular points.
+The spectral efficiency of the channel is defined as
-=== Limitations of EM.Cube's SBR Solver ===
+<math> \eta = \log_2 \left( 1 + \frac{S}{N} \right)  </math>
-It is very important to keep in mind that SBR is an asymptotic electromagnetic analysis technique that is based on Geometrical Optics (GO) and the Uniform Theory of Diffraction (UTD). It is not a &quot;full-wave&quot; technique, and it does not solve Maxwell's equations directly or numerically. SBR makes a number of assumptions, chief among them, a very high operational frequency such that the length scales involved are much larger than the operating wavelength. Under this assumed regime, electromagnetic waves start to behave like optical rays. Virtually all the calculations in SBR are based on far field approximations.
+The quantity E<sub>b</sub>/N<sub>0</sub> is the ratio of energy per bit to noise power spectral density. It is a measure of SNR per bit and is calculated from the following equation:
-In order to maintain a high computational speed for urban propagation problems, EM.Cube's SBR solver ignores double diffractions. Recall that diffractions from edges give rise to a large number of new secondary rays. The power of diffracted rays drops much faster than reflected rays. EM.Cube ignores diffracted rays that are not detected by any receiver. In other words, an edge-diffracted ray does not diffract again from another edge. However, reflected and penetrated rays do get diffracted from edges just as rays emanated directly from the sources do.
+<math> \frac{E_b}{N_0} = \frac{ 2^\eta - 1}{\eta}  </math>
-== Anatomy Of A Propagation Scene ==
+where &eta; is the spectral efficiency.
-An EM.Cube propagation scene typically consists of several elements. At a minimum, you need a transmitter (Tx) at some location to launch rays into the scene and a receiver (Rx) at another location to receive and collect the incoming rays. A transmitter and a receiver together make the simplest propagation scene, representing a free-space line-of-sight (LOS) channel. A transmitter is one of EM.Cube's several source types, while a receiver is one of EM.Cube's several observable types. A simpler source type is a Hertzian dipole. A simpler observable is a field sensor that is used to compute the electric and magnetic fields on a specified plane.
+The relationship between the bit error rate and E<sub>b</sub>/N<sub>0</sub> depends on the modulation scheme and detection type (coherent vs. non-coherent). For example, for coherent QPSK modulation, one can write:
-An outdoor propagation scene may involve several buildings (modeled as impenetrable surfaces) and an underlying flat ground or irregular terrain surface. An indoor propagation scene may involve several walls (modeled as thin penetrable surfaces), a ceiling and a floor arranged according to a certain floor plan. You can also build mixed scenes involving both impenetrable and penetrable blocks, possibly along with irregular terrain surfaces. Your sources and observables can be placed anywhere in the scene. Your transmitters and receivers can be placed outdoors or indoors. A complete list of the various elements of a propagation scene is given in the '''Physical Structure''' section of [[Propagation Module]]'s Navigation Tree as follows:
+<math> P_b = 0.5 \; \text{erfc} \left( \sqrt{ \frac{E_b}{N_0} } \right)  </math>
+where P<sub>b</sub> is the bit error rate and erfc(x) is the complementary error function:
-* Impenetrable Surfaces
+<math> \text{erfc}(x) = 1-\text{erf}(x) = \frac{2}{\sqrt{\pi}} \int_{x}^{\infty} e^{-t^2} dt  </math>
-* Penetrable Surfaces
-* Terrain Surfaces
-* Base Points
-Impenetrable, penetrable and terrain surfaces all obstruct the propagation of electromagnetic waves (rays) in the free space. What differentiates them is the types of physical phenomena that are used to model their interaction with the impinging rays. Base points are simply used to define transmitter and receiver locations in the scene. The following sections of this manual will describe each of these elements in detail.
+The '''Minimum Required SNR''' parameter is used to determine link connectivity between each transmitter and receiver pair. If you check the box labeled '''Generate Connectivity Map''' in the receiver set property dialog, a binary map of the propagation scene is generated by EM.Terrano, in which one color represents a closed link and another represent no connection depending on the selected color map type of the graph. EM.Terrano also calculates the '''Max Permissible BER''' corresponding to the specified minimum required SNR and displays it in the receiver set property dialog.
-[[File:PROP14(1).png]]
+=== A Note on EM.Terrano's Native Dipole Radiators ===
-Figure 1: The Navigation Tree of EM.Cube's [[Propagation Module]].
+When you define a new transmitter set or a new receiver set, EM.Terrano assigns a vertically polarized half-wave dipole radiator to the set by default. The radiation pattern of this native dipole radiators is calculated using well-know expressions that are derived based on certain assumptions and approximations. For example, the far-zone electric field of a vertically-polarized dipole antenna can be expressed as:
-=== The Various Types Of Surfaces &amp; Blocks ===
+<math> E_\theta(\theta,\phi) \approx j\eta_0 I_0 \frac{e^{-jk_0 r}}{2\pi r} \left[ \frac{\text{cos} \left( \frac{k_0 L}{2}  \text{cos} \theta \right) - \text{cos} \left( \frac{k_0 L}{2} \right)   }{\text{sin}\theta} \right]  </math>
-In a SBR simulation, the propagating rays hit the surface of building structures, walls, terrain (or global ground) and bounce back into the scene (reflection). Some rays penetrate thin walls or other penetrable surfaces and continue their path on the other side of the surface (transmission). The field intensity, phase and power of the reflected and transmitted rays depend on the material properties of the obstructing surface. The specular surface can be modeled as a simple homogeneous dielectric half-space or as a multilayer structure. In that respect, the buildings, walls, terrain or even the global ground all behave in a similar way:
+<math> E_\phi(\theta,\phi) \approx 0  </math>
-* They terminate an impinging ray and replace it with one or more new rays.
+where k<sub>0</sub> = 2&pi;/&lambda;<sub>0</sub> is the free-space wavenumber, &lambda;<sub>0</sub> is the free-space wavelength, &eta;<sub>0</sub> =  120&pi; &Omega; is the free-space intrinsic impedance, I<sub>0</sub> is the current on the dipole, and L is the length of the dipole.
-* They represent a specular interface between two media of different material compositions for calculating the reflection, transmission and possibly diffraction coefficients.
-EM.Cube has generalized the concept of '''Block''' as any object that obstructs and affects radio wave propagation. Rays hit the facets of a block and bounce off the surface of those facets or penetrate them and continue their propagation. Rays also get diffracted off the edges of these blocks. In EM.Cube's [[Propagation Module]], blocks are grouped together by the type of their interaction with rays. EM.Cube currently offers three types of blocks for use in a propagation scene:
+The directivity of the dipole antenna is given be the expression:
-# '''Impenetrable Surfaces:''' Rays hit the facets of this type of blocks and bounce back, but they do not penetrate the object. It is assumed that the interior of such blocks or buildings are highly absorptive.
+<math> D_0 \approx \frac{2}{F_1(k_0L) + F_2(k_0L) + F_3(k_0L)} \left[ \frac{\text{cos} \left( \frac{k_0 L}{2}  \text{cos} \theta \right) - \text{cos} \left( \frac{k_0 L}{2} \right)   }{\text{sin}\theta} \right]^2  </math>
-# '''Penetrable Surfaces:''' These blocks represent thin surfaces that are used to model the exterior and interior walls of buildings based on the &quot;Thin Wall Approximation&quot;. Rays reflect off the surface of penetrable surfaces and diffract off their edges. They also penetrate such thin surfaces and continue their paths on the other side of the wall.
-# '''Terrain Surfaces:''' These blocks are used to provide one or more impenetrable, ground surfaces for the propagation scene. Rays simply bounce off terrain objects. The global ground acts as a flat super-terrain that covers the bottom of the entire computational domain.
-EM.Cube's [[Propagation Module]] allows you to define block groups of each of the above three types. Each block group has the same color or texture and its members share the same material properties: permittivity &epsilon;<sub>r</sub> and conductivity &sigma;. Also, all the penetrable surfaces belonging to the same block group have the same wall thickness. You can define many different block groups with certain properties and underneath each introduce many member objects with different geometrical shapes and dimensions. The table below summarizes the characteristics of each block type:
+with
-{| class="wikitable"
+<math> F_1(x) = \gamma + \text{ln}(x) - C_i(x)  </math>
-|-
-! scope="col"| Block Type
-! scope="col"|Physical Effects
-! scope="col"|Admissible Object Types
-|-
-| Impenetrable Surface
-| Reflection, Diffraction
-| All Solid &amp; Surface CAD Objects
-|-
-| Penetrable Surface
-| Reflection, Diffraction, Transmission
-| All Solid &amp; Surface CAD Objects
-|-
-| Terrain Surface
-| Reflection
-| Tessellated Objects Only
-|}
-=== Impenetrable Surfaces For Outdoor Scenes ===
+<math> F_2(x) = \frac{1}{2} \text{sin}(x) \left[ S_i(2x) - 2S_i(x)  \right]  </math>
-In outdoor propagation scenes such as &quot;Urban Canyons&quot;, you are primarily interested in the wireless coverage in the areas among buildings. You can assume that rays bounce off the exterior walls of these buildings but do not penetrate them. In other words, you ignore the transmitted rays and assume that they are either absorbed or diffused inside the buildings. This is not an unrealistic assumption. EM.Cube offers &quot;Impenetrable Blocks&quot; to model buildings in outdoor propagation scenes. A penetrable block has a color or texture property as well as material properties: permittivity (e<sub>r</sub>) and conductivity (s). By default, a brick building is assumed with &epsilon;<sub>r</sub> = 4.4 and &sigma; = 0.001 S/m. Impinging rays are reflected from the facets of impenetrable buildings or diffracted from their edges.
+<math> F_3(x) = \frac{1}{2} \text{cos}(x) \left[ \gamma + \text{ln}(x/2) + C_i(2x) - 2C_i(x)  \right]  </math>
-To define a new impenetrable block group, follow these steps:
-# Right click on either the '''Impenetrable Surfaces''' item of the Navigation Tree and select '''Insert New Block...''' A dialog for setting up the block properties opens up offering a preloaded material type (Brick) with predefined color and texture.
+where &gamma; = 0.5772 is the Euler-Mascheroni constant, and C<sub>i</sub>(x) and S<sub>i</sub>(x) are the cosine and sine integrals, respectively:
-# Specify a name for the block group and select a color or texture.
-# The electromagnetic model that determines ray-block interaction is selected under '''Specular Interface Type'''. Two options are available: '''Standard Material''' or '''User Defined Model'''. The former is the default choice and requires material properties, '''Permittivity''' (&epsilon;<sub>r</sub>) and '''Electric Conductivity''' (&sigma;), which are set to &quot;Brick&quot; by default. No magnetic properties are allowed for blocks.
-# Click the '''OK''' button of the dialog to accept the changes and close it.
-[[File:PROP14(2).png]]
-Figure 1: [[Propagation Module]]'s Impenetrable Surface dialog.
+<math> C_i(x) = - \int_{x}^{\infty} \frac{ \text{cos} \tau}{\tau} d\tau  </math>
-Under an impenetrable block group, you can draw any of EM.Cube's native solid or [[Surface Objects|surface objects]] or you can import external model files like STEP, IGES or STL. You can change the properties of an impenetrable surface. In the property dialog of the surface group, click on the table that list the properties to select and highlight a row. Then, click the '''Add/Edit''' button to open up the &quot;Edit Layer&quot; dialog. In this dialog, you can change the name of the material and its permittivity and electric conductivity. The box labeled &quot;Specify Loss Tangent&quot; is unchecked by default. If you check it, you can specify the '''Loss Tangent''' of the material, which, in turn, updates the value of electric conductivity at the center frequency of the project. You can also use EM.Cube's Material List, which will  be explained later.
+<math> S_i(x) = \int_{0}^{x} \frac{ \text{sin} \tau}{\tau} d\tau  </math>
-[[File:PROP23.png]]
-Figure 2: [[Propagation Module]]'s &quot;Edit Layer&quot; dialog corresponding to impenetrable surfaces.
+In the case of a half-wave dipole, L = &lambda;<sub>0</sub>/2, and D<sub>0</sub> = 1.643. Moreover, the input impedance of the dipole antenna is Z<sub>A</sub> =  73 + j42.5 &Omega;. These dipole radiators are connected via 50&Omega; transmission lines to a 50&Omega; source or load. Therefore, there is always a certain level of impedance mismatch that violates the conjugate match condition for maximum power.
-=== Penetrable Surfaces For Indoor Scenes ===
+<table>
+<tr>
+<td> [[File:Dipole radiators.png|thumb|720px|EM.Terrano's native half-wave dipole transmitter and receiver.]] </td>
+</tr>
+</table>
-A typical indoor propagation scene usually involves an arrangement of walls that represent the interior of a building. The transmitters and receivers are then placed in the spaces among such walls. From the point of view of EM.Cube's SBR simulator, walls act like thin penetrable surfaces. EM.Cube uses the &quot;Thin Wall Approximation&quot; to model penetrable surfaces. It assumes that rays simply penetrate a wall and exit at the same specular point on the opposite side of the wall. In other words, rays are not displaced by the walls, nor do they get trapped inside the walls (no internal reflection). This is equivalent to assuming a zero thickness for penetrable surfaces for the purpose of geometrical ray tracing, while the finite thickness of the &quot;thin&quot; surface is used for electromagnetic calculation of transmission coefficient. EM.Cube offers &quot;Penetrable Surface Blocks&quot; for the construction of rooms in indoor propagation scenes as well as modeling of hollow buildings and other structures. You can define many penetrable surface groups with arbitrary thicknesses and material properties (color, texture, permittivity and electric conductivity).
+On the other hand, we you specify a user-defined antenna pattern for the transmitter or receiver sets, you import a 3D radiation pattern file that contains all the values of E<sub>&theta;</sub> and E<sub>&phi;</sub> for all the combinations of (&theta;, &phi;) angles. Besides the three native dipole radiators, [[EM.Cube]] also provides 3D radiation pattern files for three X-, Y- and Z-polarized half-wave resonant dipole antennas. These pattern data were generated using a full-wave solver like [[EM.Libera]]'s wire MOM solver. The names of the radiation pattern files are:
-To define a new penetrable surface group, follow these steps:
+* DPL_STD_X.RAD
+* DPL_STD_Y.RAD
+* DPL_STD_Z.RAD
-# Right click on one of the '''Penetrable Surfaces''' item in the Navigation Tree and select '''Insert New Block...''' A dialog for setting up the wall properties opens up offering a preloaded material type (Brick) with predefined color and texture.
+and they are located in the folder "\Documents\EMAG\Models" on your computer. Note that these are full-wave simulation data and do not involve any approximate assumptions. To use these files as an alternative to the native dipole radiators, you need to select the '''User Defined Antenna Pattern''' radio button as the the radiator type in the transmitter or receiver set property dialog.
-# Specify a name for the surface group and select a color or texture.
-# The properties of a penetrable surface are identical to those of an impenetrable surface, plus an additional thickness property.
-# By default, a brick wall with a thickness of 0.5 units is assumed. You can change the '''Thickness''' of the penetrable surface as well as its '''Permittivity'''  &epsilon;<sub>r</sub> and '''Electric Conductivity''' &sigma;.
-# Click the '''OK''' button of the dialog to accept the changes and close it.
-[[File:PROP15(1).png]]
+=== A Note on the Rotation of Antenna Radiation Patterns ===
-Figure 1: [[Propagation Module]]'s Penetrable Surface dialog.
+EM.Terrano's Transmitter Set dialog and Receiver Set dialog both allow you to rotate an imported radiation pattern. In that case, you need to specify the '''Rotation''' angles in degrees about the X-, Y- and Z-axes. It is important to note that these rotations are performed sequentially and in the following order: first a rotation about the X-axis, then a rotation about the Y-axis, and finally a rotation about the Z-axis. In addition, all the rotations are performed with respect to the "rotated" local coordinate systems (LCS). In other words, the first rotation with respect to the local X-axis transforms the XYZ LCS to a new primed X<sup>&prime;</sup>Y<sup>&prime;</sup>Z<sup>&prime;</sup> LCS. The second rotation is performed with respect to the new Y<sup>&prime;</sup>-axis and transforms the X<sup>&prime;</sup>Y<sup>&prime;</sup>Z<sup>&prime;</sup> LCS to a new double-primed X<sup>&prime;&prime;</sup>Y<sup>&prime;&prime;</sup>Z<sup>&prime;&prime;</sup> LCS. The third rotation is finally performed with respect to the new Z<sup>&prime;&prime;</sup>-axis. The figures below shows single and double rotations.
-Under a penetrable surface group, you can draw any of EM.Cube's native solid or [[Surface Objects|surface objects]] or you can import external model files like STEP, IGES or STL. You can change the properties of a penetrable surface group including its default thickness. In the property dialog of the surface group, click on the table that list the properties to select and highlight a row. Then, click the '''Add/Edit''' button to open up the &quot;Edit Layer&quot; dialog. Similar to the case of impenetrable surfaces, from this dialog, you can change the material properties (permittivity and electric conductivity) as well as '''Thickness''', which is expressed in the project units. You can also use EM.Cube's Material List, which will be explained later.
+<table>
+<tr>
+<td> [[File:PROP22B.png|thumb|300px|The local coordinate system of a linear dipole antenna.]] </td>
+<td> [[File:PROP22C.png|thumb|600px|Rotating the dipole antenna by +90&deg; about the local Y-axis.]] </td>
+</tr>
+</table>
+<table>
+<tr>
+<td> [[File:PROP22D.png|thumb|720px|Rotating the dipole antenna by +90&deg; about the local X-axis and then by -45&deg; by the local Y-axis.]] </td>
+</tr>
+</table>
-[[File:PROP25.png]]
+=== Adjustment of Tx/Rx Elevation above a Terrain Surface ===
-Figure 2: [[Propagation Module]]'s &quot;Edit Layer&quot; dialog corresponding to penetrable surfaces.
+When your transmitters or receivers are located above a flat terrain like the global ground, their Z-coordinates are equal to their height above the ground, as the terrain elevation is fixed and equal to zero everywhere. In many propagation modeling problems, your transmitters and receivers may be located above an irregular terrain with varying elevation across the scene. In that case, you may want to place your transmitters or receivers at a certain height above the underlying ground. The Z-coordinate of a transmitter or receiver is now the sum of the terrain elevation at the base point and the specified height. EM.Terrano gives you the option to adjust the transmitter and receiver sets to the terrain elevation. This is done for individual transmitter sets and individual receiver sets. At the top of the Transmitter Dialog there is a check box labeled &quot;'''Adjust Tx Sets to Terrain Elevation'''&quot;. Similarly, at the top of the Receiver Dialog there is a check box labeled &quot;'''Adjust Rx Sets to Terrain Elevation'''&quot;. These boxes are unchecked by default. As a result, your transmitter sets or receiver sets coincide with their associated base points in the project workspace. If you check these boxes and place a transmitter set or a receiver set above an irregular terrain, the transmitters or receivers are elevated from the location of their associated base points by the amount of terrain elevation as can be seen in the figure below.
-You can construct several thin walls and arrange them as rooms. A regular room can be built by placing four vertical wall objects together with an optional horizontal wall at the top for the ceiling. Alternatively, you may use EM.Cube's hollow box objects or boxes with one or two capped end(s).  '''Keep in mind that all the penetrable surfaces belonging to a group have the same wall thickness, which is initially set to 0.5 project units by default. Also, note that solid CAD objects belonging to a penetrable surface group are treated as air-filled hollow structures.''' The thickness of penetrable surfaces is implied and not visualized when displaying objects in the project workspace.
+To better understand why there are two separate sets of points in the scene, note that a point array (CAD object) is used to create a uniformly spaced base set. The array object always preserves its grid topology as you move it around the scene. However, the transmitters or receivers associated with this point array object are elevated above the irregular terrain and no longer follow a strictly uniform grid. If you move the base set from its original position to a new location, the base points' topology will stay intact, while the associated transmitters or receivers will be redistributed above the terrain based on their new elevations.
-=== Computational Domain &amp; Global Ground ===
+<table>
+<tr>
+<td>
+[[Image:PROP MAN8.png|thumb|left|640px|A transmitter (red) and a grid of receivers (yellow) adjusted above a plateau terrain surface. The underlying base point sets (blue and orange dots) associated with the adjusted transmitters and receivers on the terrain are also visible in the figure.]]
+</td>
+</tr>
+</table>
-The SBR simulation engine requires a finite computational domain. All the stray rays that hit the boundaries of this finite domain are terminated during the simulation process. Such rays exit the computational domain and travel to the infinity, with no chance of ever reaching any receiver in the scene. When you define a propagation scene with various elements like buildings, walls, terrain, etc., a dynamic domain is automatically established and displayed as a wireframe box with green lines that surrounds the entire scene. Every time you create a new object, the domain is automatically adjusted and extended to enclose all the objects in the scene. You can change the size and color of the domain box through the Ray Domain Settings Dialog, which can be accessed in one of the following three ways:
+== Discretizing the Propagation Scene in EM.Terrano ==
-# Click the '''Domain''' [[File:image025.jpg]] button of the Simulation Toolbar.
+=== Why Do You Need to Discretize the Scene? ===
-# Select the '''Simulate''' &gt; '''Computational Domain''' &gt; '''Settings...''' item of the Simulate Menu.
-# Right click on the '''Ray Domain''' item of the Navigation Tree and select '''Domain Settings...'''
-# Use the keyboard shortcut '''Ctrl + A'''.
-The size of the Ray domain is specified in terms of six '''Offset''' parameters along the ±X, ±Y and ±Z directions. The default value of all these six offset parameters is 10 project units. You can change them arbitrarily. After changing these values, use the '''Apply''' button to make the changes effective while the dialog is still open.
+EM.Terrano's SBR solver uses a method known as Geometrical Optics (GO) in conjunction with the Uniform Theory of Diffraction (UTD) to trace the rays from their originating point at the source to the individual receiver locations. Rays may hit obstructing objects on their way and get reflected, diffracted or transmitted. EM.Terrano's SBR solver can only handle diffraction off linear edges and reflection from and transmission through planar interfaces. When an incident ray hits the surface of the obstructing object, a local planar surface assumption is made at the specular point. The assumptions of linear edges and planar facets obviously work in the case of a scene  with cubic buildings and a flat global ground.
-[[File:PROP15.png]]
+In many practical scenarios, however, your buildings may have curved surfaces, or the terrain may be irregular. EM.Terrano allows you to draw any type of surface or solid geometric objects such as cylinders, cones, etc. under impenetrable and penetrable surface groups or penetrable volumes. EM.Terrano's mesh generator creates a triangular surface mesh of all the objects in your propagation scene, which is called a facet mesh. Even the walls of cubic buildings are meshed using triangular cells. This enables EM.Terrano to properly discretize composite buildings made of conjoined cubic objects.
-Figure 1: [[Propagation Module]]'s Domain Settings dialog.
+Unlike [[EM.Cube]]'s other computational modules, the density or resolution of EM.Terrano's surface mesh does not depend on the operating frequency and is not expressed in terms of the wavelength. The sole purpose of EM.Terrano's facet mesh is to discretize curved and irregular scatterers into flat facets and linear edges. Therefore, geometrical fidelity is the only criterion for the quality of a facet mesh. It is important to note that discretizing smooth objects using a triangular surface mesh typically creates a large number of small edges among the facets that are simply mesh artifacts and should not be considered as diffracting edges. For example, each rectangular face of a cubic building is subdivided into four triangles along the two diagonals. The four internal edges lying inside the face are obviously not diffracting edges. A lot of subtleties like these must be taken into account by the SBR solver to run accurate and computationally efficient simulations.
-Most outdoor and indoor propagation scenes include a flat ground at their bottom, which bounces incident rays back into the scene. EM.Cube's [[Propagation Module]] provides a global flat ground at z = 0. The global ground indeed acts as an impenetrable surface that blocks the entire computational domain from the z = 0 plane downward. It is displayed as a translucent green plane at z = 0 extending downward. The color of the ground plane is always the same as the color of the ray domain. The global ground is assumed to be made of a homogeneous dielectric material with a specified permittivity &epsilon;<sub>r</sub> and electric conductivity &sigma;. By default, a rocky ground is assumed with &epsilon;<sub>r</sub> = 5 and &sigma; = 0.005 S/m. You can remove the global ground, in which case, you will have a free space scene. To disable the global ground, open up the Global Ground Settings Dialog, which can be accessed by right clicking on the '''Global Ground''' item in the Navigation Tree and selecting '''Global Ground Settings... '''Remove the check mark from the box labeled '''&quot;Include Half-Space Ground (z&lt;0)&quot;''' to disable the global ground. This will also remove the green translucent plane from the bottom of your scene. You can also change the material properties of the global ground and set new values for the permittivity and electric conductivity of the impenetrable, half-space, dielectric medium. '''Do not forget to disable the global ground if you want to model a free space propagation scene.'''
+=== Generating the Facet Mesh ===
-[[File:PROP4.png]]
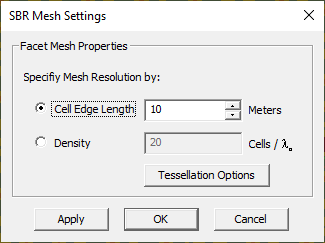
+You can view and examine the discretized version of your scene's objects as they are sent to the SBR simulation engine. You can adjust the mesh resolution and increase the geometric fidelity of discretization by creating more and finer triangular facets. On the other hand, you may want to reduce the mesh complexity and send to the SBR engine only a few coarse facets to model your buildings. The resolution of EM.Terrano's facet mesh generator is controlled by the '''Cell Edge Length''' parameter, which is expressed in project length units. The default mesh cell size of 100 units might be too large for non-flat objects. You may have to set a smaller cell edge length in EM.Terrano's Mesh Settings dialog, along with a lower curvature angle tolerance value to capture the curvature of your curved structures adequately.
-Figure 2: [[Propagation Module]]'s Global Ground Settings dialog.
+<table>
+<tr>
+<td>
+[[Image:prop_manual-29.png|thumb|left|480px|EM.Terrano's mesh settings dialog.]]
+</td>
+</tr>
+</table>
-=== Terrain Surfaces vs. Global Ground ===
+[[Image:Info_icon.png|30px]] Click here to learn more about '''[[Preparing_Physical_Structures_for_Electromagnetic_Simulation#Working_with_EM.Cube.27s_Mesh_Generators | Working with Mesh Generator]]'''.
-A terrain surface acts as a custom, unlevel or irregular ground for your propagation scene. EM.Cube's default global ground blocks the z &lt; 0 half-space everywhere in the computational domain. You can simply turn off the global ground and create one or more terrain objects and place them arbitrarily in the scene. You can also import an external terrain model or file. A terrain represents an impenetrable surface with a more complex surface profile. You can have one or more terrain objects of finite extents and place them on or above the global ground.
+[[Image:Info_icon.png|30px]] Click here to learn more about the properties of '''[[Glossary_of_EM.Cube%27s_Simulation-Related_Operations#Facet_Mesh | EM.Terrano's Facet Mesh Generator]]'''.
-Terrain objects have some important differences with objects of the &quot;Impenetrable Surface&quot; type:
+<table>
+<tr>
+<td> [[Image:UrbanCanyon2.png|thumb|left|640px|The facet mesh of the buildings in the urban propagation scene generated by EM.Terrano's Random City wizard with a cell edge length of 100m.]] </td>
+</tr>
+<tr>
+<td> [[Image:UrbanCanyon3.png|thumb|left|640px|The facet mesh of the buildings in the urban propagation scene generated by EM.Terrano's Random City wizard with a cell edge length of 10m.]] </td>
+</tr>
+</table>
-# While impenetrable blocks can be created using any of EM.Cube's solid or surface CAD object creation tools, terrain objects are created either using EM.Cube's '''Terrain Generator''' or by importing an external terrain file.
+== Running Ray Tracing Simulations in EM.Terrano ==
-# Terrain objects belong to a special type of CAD objects called &quot;Tessellated Objects&quot;, which differ from other regular CAD [[Surface Objects|surface objects]] or EM.Cube's polymesh surfaces.
-# Terrain surfaces do not diffract impinging rays at their many small edges.
-# Terrain objects affect the elevation of other objects or transmitters or receivers that are located above them.
-Just as other blocks are grouped by their color, texture and material composition, terrain objects are also grouped in a similar fashion. Before you can generate or import a new terrain object, first you have to define a terrain group and specify its color/texture and material properties. To define a new terrain group, follow these steps:
+EM.Terrano provides a number of different simulation or solver types:
-* Right click on the '''Terrain''' item in the Navigation Tree and select '''Insert New Terrain...''' A dialog for setting up the terrain properties opens up offering a of preloaded material type (Rock) with predefined green color and no texture.
+* 3D Field Solver
-* Specify a name for the terrain group and select a color or texture.
+* SBR Channel Analyzer
-* Similar to other blocks, you have to specify the material properties, Permittivity (&epsilon;<sub>r</sub>) and Electric Conductivity (&sigma;), of the terrain group. Rock with &epsilon;<sub>r</sub> = 5 and &sigma; = 0.005 S/m is the default material choice for a new terrain.
+* Log-Haul Channel Analyzer
-* Click the '''OK''' button of the dialog to accept the changes and close it.
+* Communication Link Solver
+* Radar Link Solver
-[[File:PROP16.png]]
+The first three simulation types are described below. For a description of EM.Terrano's Radar Simulator, follow this link.
-Figure 1: [[Propagation Module]]'s Terrain dialog.
+=== Running a Single-Frequency SBR Analysis ===
-You can change the properties of a terrain surface group from its property dialog. Click on the table that list the properties to select and highlight a row. Then, click the '''Add/Edit''' button to open up the &quot;Edit Layer&quot; dialog, which is identical to the case of impenetrable surfaces. You can also use EM.Cube's Material List, which will be explained later. When a new terrain type is created, its node on the Navigation Tree becomes active. Under this node you can create and add new terrain objects. When a terrain node is active for drawing, all CAD object creation tools are disabled. You have three options for creating a new terrain object, which will be described in detail in the next sections of this manual:
+Its main solver is the '''3D SBR Ray Tracer'''. Once you have set up your propagation scene in EM.Terrano and have defined sources/transmitters and observables/receivers for your scene, you are ready to run a SBR ray tracing simulation. You set the simulation mode in EM.Terrano's simulation run dialog. A single-frequency SBR analysis is a single-run simulation and the simplest type of ray tracing simulation in EM.Terrano. It involves the following steps:
-# Use EM.Cube's '''Terrain Generator'''.
+* Set the units of your project and the frequency of operation. Note that the default project unit is '''millimeter'''. Wireless propagation problems usually require meter, mile or kilometer as the project unit.
-# Import an external terrain file of &quot;'''.TRN'''&quot; type.
+* Create the blocks and draw the buildings at the desired locations.
-# Import an external terrain file of &quot;'''.DEM'''&quot; type.
+* Keep the default ray domain and accept the default global ground or change its material properties.
+* Define an excitation source and observables for your project.
+* If you intend to use transmitters and receivers in your scene, first define the required base sets and then define the transmitter and receiver sets based on them.
+* Run the SBR simulation engine.
+* Visualize the coverage map and plot other data.
-=== Using Terrain Generator ===
+You can access EM.Terrano's Simulation Run dialog by clicking the '''Run''' [[File:run_icon.png]] button of the '''Simulate Toolbar''' or by selecting '''Simulate &rarr; Run...''' or using the keyboard shortcut {{key|Ctrl+R}}. When you click the {{key|Run}} button, a new window opens up that reports the different stages of the SBR simulation and indicates the progress of each stage. After the SBR simulation is successfully completed, a message pops up and prompts the completion of the process.
-[[File:PROP18.png|thumb|250px|[[Propagation Module]]'s Terrain Generator dialog]]
+<table>
+<tr>
+<td>
+[[Image:Terrano L1 Fig16.png|thumb|left|480px|EM.Terrano's simulation run dialog.]]
+</td>
+</tr>
+</table>
-EM.Cube provides a convenient and powerful Terrain Generator for creating a variety of terrain [[Surface Objects|surface objects]]. EM.Cube's Terrain Generator looks very similar to [[CubeCAD]]'s Surface Generator. However, whereas the Surface Generator creates a generic or polymesh surface object, Terrain Generator always creates another special type of object known as a '''Tessellated Object'''. A terrain object is much simpler than EM.Cube's polymesh objects and is usually made up of triangular or quadrilateral facets. As such, terrain objects have limited editing capabilities. For example, you can cut, copy, paste, translate or rotate  terrain objects. But operations like scaling, mirroring, grouping (composite), arraying, exploding, linking or Boolean operations do not work on terrain objects.
+<table>
+<tr>
+<td>
+[[Image:PROP MAN10.png|thumb|left|550px|EM.Terrano's output message window.]]
+</td>
+</tr>
+</table>
-To create a new terrain object using Terrain Generator, first you need to define a terrain group in the Navigation Tree. Right click on the name of the terrain node and select '''Terrain Generator...''' from the contextual menu. This opens up the Terrain Generator Dialog. Using Terrain Generator, you can build a single terrain surface or an array of surfaces patched together. Some of the available terrain models include:
+=== Changing the SBR Engine Settings ===
-# Flat Plane
+There are a number of SBR simulation settings that can be accessed and changed from the Ray Tracing Engine Settings Dialog. To open this dialog, click the button labeled {{key|Settings}} on the right side of the '''Select Simulation or Solver Type''' drop-down list in the Run Dialog. EM.Terrano's SBR simulation engine allows you to separate the physical effects that are calculated during a ray tracing process. You can selectively enable or disable '''Reflection/Transmission''' and '''Edge Diffraction''' in the "Ray-Block Interactions" section of this dialog. By default, ray reflection and transmission and edge diffraction effects are enabled. Separating these effects sometimes help you better analyze your propagation scene and understand the impact of various blocks in the scene.
-# Hill (Elliptic Quadratic)
-# Mountain (Elliptic Cone)
-# 1-D and 2-D Cliff
-# Gaussian Hump
-# Undulated Sinusoid
-# Undulated Sinc
-# Super-quadratic Plateau
-# Custom Function
-# XY Grid Data
-In all of the above models, you can set the height of the surface object to an any desired value. You set the lateral extents of the surface and its resolution along the X and Y directions in the boxes labeled '''Range Start''', '''Range Stop''' and '''Range Step'''. The step values along the X and Y directions are a measure of surface smoothness: the smaller the step values, the higher the resolution and the smoother the resulting terrain object.
+EM.Terrano allows a finite number of ray bounces for each original ray emanating from a transmitter. This is very important in situations that may involve resonance effects where rays get trapped among multiple surfaces and may bounce back and forth indefinitely. This is set using the box labeled &quot;'''Max No. Ray Bounces'''&quot;, which has a default value of 10. Note that the maximum number of ray bounces directly affects the computation time as well as the size of output simulation data files. This can become critical for indoor propagation scenes, where most of the rays undergo a large number of reflections. Two other parameters control the diffraction computations: '''Max Wedge Angle''' in degrees and '''Min Edge Length''' in project units. The maximum wedge angle is the angle between two conjoined facets that is considered to make them almost flat or coplanar with no diffraction effect. The default value of the maximum wedge angle is 170&deg;. The minimum edge length is size of the common edge between two conjoined facets that is considered as a mesh artifact and not a real diffracting edge. The default value of the minimum edge length is one project units.
-Some surface types have an additional shape factor called '''Alpha''' that is identical to the alpha parameter in the surface generator. For example, a Gaussian Hump is defined as exp(-r<sup>2</sup>/(2a<sup>2</sup>)), where r is the polar radius. For a Super-quadratic Hump, the input parameter a defines the degree of the super-quadratic surface. a = 2 corresponds to an ellipsoid. Larger values of a get close to a rectangular base with rounded corners. An undulated sinusoidal surface is defined by cos(pax/D<sub>x</sub>)*cos(pay/D<sub>y</sub>), and an undulated sinc is defined by D<sub>x</sub>*D<sub>y</sub>*sin(pax/D<sub>x</sub>)*sin(pay/D<sub>x</sub>)/(2pxy), where D<sub>x</sub> and D<sub>y</sub> are the X and Y dimensions, respectively. Terrain Generator creates a unit cell based on the specified surface type. From the same dialog, you can also produce an array arrangement of such unit cells. Simply enter any number of elements along the X and Y directions in the boxes labeled '''Array'''.
+<table>
+<tr>
+<td>
+[[Image:PROP MAN11.png|thumb|left|720px|EM.Terrano's SBR simulation engine settings dialog.]]
+</td>
+</tr>
+</table>
-[[File:PROP19.png|800px]]
+As rays travel in the scene and bounce from surfaces, they lose their power, and their amplitudes gradually diminish. From a practical point of view, only rays that have power levels above the receiver sensitivity can be effectively received. Therefore, all the rays whose power levels fall below a specified power threshold are discarded. The '''Ray Power Threshold''' is specified in dBm and has a default value of -150dBm. Keep in mind that the value of this threshold directly affects the accuracy of the simulation results as well as the size of the output data file.
-Figure: A 4 × 4 array of hill terrain objects.
+You can also set the '''Ray Angular Resolution''' of the transmitter rays in degrees. By default, every transmitter emanates equi-angular ray tubes at a resolution of 1 degree. Lower angular resolutions larger than 1° speed up the SBR simulation significantly, but they may compromise the accuracy. Higher angular resolutions less than 1° increase the accuracy of the simulating results, but they also increase the computation time. The SBR Engine Settings dialog also displays the '''Recommended Ray Angular Resolution''' in degrees in a grayed-out box. This number is calculated based on the overall extents of your computational domain as well as the SBR mesh resolution. To see this value, you have to generate the SBR mesh first. Keeping the angular resolution of your project above this threshold value makes sure that the small mesh facets at very large distances from the source would not miss any impinging ray tubes during the simulation.
-You can define any arbitrary surface by entering an equation of the two [[variables]] x and y as z = f(x,y). In this case, you have to select the '''Custom Function''' option in the dropdown list labeled '''Model'''. You should enter your equation as any mathematical expression in the box labeled '''Function f(x,y)'''. You can use any of EM.Cube's mathematical functions listed in the '''Function Dialog''' or combine several of them. Note that after selecting the custom function option, the height of the surface is determined by your equation, and the '''Height''' box is disabled. You can also introduce random noise and create a rough terrain. You can do this by setting a nonzero value for '''Noise''', which represent the RMS peak-to-valley amplitude of the surface roughness. The figures below show two custom terrain surfaces modeled by the equation z = (x.y)/20 defined over the range [0, 10] in both X and Y directions. Random noise has been added to both surfaces, with the noise amplitude being 0.2 and 0.5 for the left and right figures, respectively.
+EM.Terrano gives a few more options for the ray tracing solution of your propagation problem. For instance, it allows you to exclude the direct line-of-sight (LOS) rays from the final solution. There is a check box for this purpose labeled "Exclude direct (LOS) rays from the solution", which is unchecked by default. EM.Terrano also allows you to superpose the received rays incoherently. In that case, the powers of individual ray are simply added to compute that total received power. This option in the check box labeled "Superpose rays incoherently" is disabled by default, too.
-[[File:PROP21.png|400px]] [[File:PROP20.png|400px]]
+At the end of a ray tracing simulation, the electric field of each individual ray is computed and reported. By default, the actual received ray fields are reported, which are independent of the radiation pattern of the receive antennas. EM.Terrano provides a check box labeled "Normalize ray's E-field based on receiver pattern", which is unchecked by default. If this box is checked, the field of each ray is normalized so as to reflect that effect of the receiver antenna's radiation pattern. The received power of each ray is calculated from the following equation:
-Figure: Two noisy custom terrain surfaces both defined as z = (x.y)/20: (Left) RMS noise amplitude = 0.2, (right) RMS noise amplitude = 0.5.
+<math> P_{ray} = \frac{ | \mathbf{E_{norm}} |^2 }{2\eta_0} \frac{\lambda_0^2}{4\pi}  </math>
-=== Generating Grid-Based Terrain ===
+It can be seen that if the ray's E-field is not normalized, the computed ray power will correspond to that of a polarization matched isotropic receiver.
-Every time you create a new terrain object using Terrain Generator, an ASCII data file named &quot;GeneratedTerrain&quot; with a &quot;'''.TRN'''&quot; file extension is created and placed in your project folder. This is EM.Cube's simple native terrain file format that basically lists all the (x, y, z) coordinates of the generated surface points on a horizontal, rectangular XY grid. Terrain Generator simply takes your custom function definition or one of the selected catalog surface types and generates the digital elevation data on the specified grid.
+=== Polarimetric Channel Analysis ===
-Another type of terrain model that the terrain generator provides is '''XY Grid Data'''. In this case, you define a rectangular XY grid with a uniform grid cell size along the X and Y directions and manually define the Z-elevation for each grid point. This is similar to the surface generator's &quot;2D Uniform Grid&quot; model type in [[CubeCAD]]. Based on your input to '''Range Start''', '''Range Stop''' and '''Range Step''' along X and Y, a 2D grid is set up and displayed in a table at the bottom of the terrain generator dialog. By default, all the Z-elevations are set to zero initially. You can click on each table cell and overwrite it with a new value. At the end, click the '''Create''' button of the dialog to add the new grid-based terrain object to the Navigation Tree.
+In a 3D SBR simulation, a transmitter shoots a large number of rays in all directions. The electric fields of these rays are polarimetric and their strength and polarization are determined by the designated radiation pattern of the transmit antenna. The rays travel in the propagation scene and bounce from the ground and buildings or other scatterers or get diffracted at the building edges until they reach the location of the receivers. Each individual ray has its own vectorial electric field and power. The electric fields of the received rays are then superposed coherently and polarimetrically to compute the total field at the receiver locations. The designated radiation pattern of the receivers is then used to compute the total received power by each individual receiver.
-[[File:terrain10_tn.png]]
+From a theoretical point of view, the radiation patterns of the transmit and receive antennas are independent of the propagation channel characteristics. For the given locations of the point transmitters and receivers, one can assume ideal isotropic radiators at these points and compute the polarimetric transfer function matrix of the propagation channel. This matrix relates the received electric field at each receiver location to the transmitted electric field at each transmitter location. In general, the vectorial electric field of each individual ray is expressed in the local standard spherical coordinate system at the transmitter and receiver locations. In other words, the polarimetric channel matrix expresses the '''E<sub>&theta;</sub>''' and '''E<sub>&phi;</sub>''' field components associated with each ray at the receiver location to its '''E<sub>&theta;</sub>''' and '''E<sub>&phi;</sub>''' field components at the transmitter location. Each ray has a delay and &theta; and &phi; angles of departure at the transmitter location and &theta; and &phi; angles of departure at the receiver location.
-A grid-based terrain object.
+To perform a polarimatric channel characterization of your propagation scene, open EM.Terrano's Run Simulation dialog and select '''Channel Analyzer''' from the drop-down list labeled '''Select Simulation or Solver Type'''. At the end of the simulation, a large ray database is generated with two data files called "sbr_channel_matrix.DAT" and "sbr_ray_path.DAT". The former file contains the delay, angles of arrival and departure and complex-valued elements of the channel matrix for all the individual rays that leave each transmitter and arrive at each receiver. The latter file contains the geometric aspects of each ray such as hit point coordinates.
-=== Importing &amp; Exporting Terrain Models ===
+=== The "Near Real-Time" Polarimatrix Solver ===
-You can import two types of terrain in EM.Cube's [[Propagation Module]]. The first type is &quot;'''.TRN&quot;''' terrain file, which is EM.Cube's native terrain format. It is a basic digital elevation map with a very simple ASCII data file format. The resolution of the terrain map in the X and Y directions is specified in meters as STEPS. The (x, y, z) coordinates of the terrain points are then listed one point per line. The other type of terrain format supported by EM.Cube is the standard '''7.5min DEM''' file format with a '''.DEM''' file extension.
+After EM.Terrano's channel analyzer generates a ray database that characterizes your propagation channel polarimetrically for all the combinations of transmitter and receiver locations, a ray tracing solution of the propagation problem can readily be found in almost real time by incorporating the effects of the radiation patterns of transmit and receive antennas. This is done using the '''Polarimatrix Solver''', which is the third option of the drop-down list labeled '''Select Simulation or Solver Type''' in EM.Terrano's Run Simulation dialog. The results of the Polarimatrix and 3D SBR solvers must be identical from a theoretical point of view. However, there might be small discrepancies between the two solutions due to roundoff errors.
-To import an external terrain model, first you have to create a terrain group node in the Navigation Tree. Right click on the name of the terrain group in the Navigation Tree and select either '''Import Terrain...''' or '''Import DEM File...''' A standard Windows '''Open Dialog''' opens up, with the file type set to .TRN or .DEM extensions, respectively. You can browse your folders and find the right terrain model file to import.
+Using the Polarimatrix solver can lead to a significant reduction of the total simulation time in sweep simulations that involve a large number of transmitters and receivers. Certain simulation modes of EM.Terrano are intended for the Polarimatrix solver only as will be described in the next section.
-You can also export all the terrain objects in the project workspace as a terrain file with a '''.TRN''' file extension. You can even import a DEM terrain model from an external file and then save and export it as a native terrain (.TRN) file. To export the terrain, select '''File''' &gt; '''Export...''' from [[Propagation Module]]'s '''File Menu'''. The standard Windows Save Dialog opens up with the default file type set to '''.TRN'''. Type in a name for your new terrain file and click the '''Save''' button to export the terrain data.
+{{Note| In order to use the Polarimatrix solver, you must first generate a ray database of your propagation scene using EM.Terrano's Channel Analyzer.}}
-[[File:prop_manual-12_tn.png|800px]]
+=== EM.Terrano's Simulation Modes ===
-Figur: An imported external terrain model.
+EM.Terrano provides a number of different simulation modes that involve single or multiple simulation runs:
-=== Multilayer Surface Models ===
+{| class="wikitable"
+|-
+! scope="col"| Simulation Mode
+! scope="col"| Usage
+! scope="col"| Which Solver?
+! scope="col"| Frequency
+! scope="col"| Restrictions
+|-
+| style="width:120px;" | [[#Running a Single-Frequency SBR Analysis | Single-Frequency Analysis]]
+| style="width:180px;" | Simulates the propagation scene "As Is"
+| style="width:150px;" | SBR, Channel Analyzer, Polarimatrix, Radar Simulator
+| style="width:120px;" | Runs at the center frequency fc
+| style="width:300px;" | None
+|-
+| style="width:120px;" | [[Parametric_Modeling_%26_Simulation_Modes_in_EM.Cube#Running_Frequency_Sweep_Simulations_in_EM.Cube | Frequency Sweep]]
+| style="width:180px;" | Varies the operating frequency of the ray tracer
+| style="width:150px;" | SBR, Channel Analyzer, Polarimatrix, Radar Simulator
+| style="width:120px;" | Runs at a specified set of frequency samples
+| style="width:300px;" | None
+|-
+| style="width:120px;" | [[Parametric_Modeling_%26_Simulation_Modes_in_EM.Cube#Running_Parametric_Sweep_Simulations_in_EM.Cube | Parametric Sweep]]
+| style="width:180px;" | Varies the value(s) of one or more project variables
+| style="width:150px;" | SBR
+| style="width:120px;" | Runs at the center frequency fc
+| style="width:300px;" | Requires definition of sweep variables, works only with SBR solver as the physical scene may change during the sweep
+|-
+| style="width:120px;" | [[#Transmitter_Sweep | Transmitter Sweep]]
+| style="width:180px;" | Activates two or more transmitters sequentially with only one transmitter broadcasting at each simulation run
+| style="width:150px;" | Polarimatrix
+| style="width:120px;" | Runs at the center frequency fc
+| style="width:300px;" | Requires at least two transmitters in the scene, works only with Polarimatrix solver and requires an existing ray database
+|-
+| style="width:120px;" | [[#Rotational_Sweep | Rotational Sweep]]
+| style="width:180px;" | Rotates the radiation pattern of the transmit antenna(s) sequentially to model beam steering
+| style="width:150px;" | Polarimatrix
+| style="width:120px;" | Runs at the center frequency fc
+| style="width:300px;" | Works only with Polarimatrix solver and requires an existing ray database
+|-
+| style="width:120px;" | [[#Mobile_Sweep | Mobile Sweep]]
+| style="width:180px;" | Considers one pair of active transmitter and receiver at each simulation run to model a mobile communication link
+| style="width:150px;" | Polarimatrix
+| style="width:120px;" | Runs at the center frequency fc
+| style="width:300px;" | Requires the same number of transmitters and receivers, works only with Polarimatrix solver and requires an existing ray database
+|}
-[[File:PROP26.png|thumb|250px|Propagation Module's Penetrable Surface Dialog showing a three-layer wall composition]]
+Click on each item in the above list to learn more about each simulation mode.
-Most of the time, your outdoor propagation scene consists of simple buildings made of single-layer walls with standard material properties (&epsilon;<sub>r</sub> and &sigma;). In the case of a single-layer impenetrable surface, the specular interface is an infinite dielectric half-space, which reflects the impinging rays. Single-layer penetrable surfaces, on the other hand, involve finite-thickness dielectric walls, which both reflect and transmit the incident rays. Similarly, most of your indoor propagation scenes involve simple single-layer penetrable walls with the specified material properties &epsilon;<sub>r</sub> and &sigma;. A thin wall acts like a finite-thickness dielectric slab that both reflects and transmits incident rays. In the case of the global ground or terrain objects, only ray reflection off the ground surface is considered.
+You set the simulation mode in EM.Terrano's simulation run dialog using the drop-down list labeled '''Simulation Mode'''. A single-frequency analysis is a single-run simulation. All the other simulation modes in the above list are considered multi-run simulations. In multi-run simulation modes, certain parameters are varied and a collection of simulation data files are generated. At the end of a sweep simulation, you can plot the output parameter results on 2D graphs or you can animate the 3D simulation data from the navigation tree.
-In EM.Cube's [[Propagation Module]], you can define multilayer surfaces with both reflection and transmission properties. You can define multilayer impenetrable buildings, multilayer penetrable walls, and multilayer terrain, with an arbitrary number of layers having different material compositions. You define a multilayer surface in the property dialog of a block, whether impenetrable, penetrable or terrain. In the section entitled '''Surface Type''', two options are available: '''Standard Material''' or '''User Defined Model'''. For simple multilayer walls, select the '''Standard Material''' option. You can add new layers with arbitrary thickness and material parameters to the existing layers. To insert a new layer, deselect any items in the layer list, and click the '''Add/Edit''' button to open the &quot;Add Layer&quot; Dialog. Here you can enter a name for the new layer and values for its '''Thickness''', &epsilon;<sub>r</sub> and &sigma;. You may also delete any layer by selecting and highlighting it and clicking the '''Delete''' button. You can move layers up or down using the '''Move Up''' and '''Move Down''' buttons and change the layer hierarchy.
+{{Note| EM.Terrano's frequency sweep simulations are very fast because the geometrical optics (ray tracing) part of the simulation is frequency-independent.}}
-You can also search EM.Cube's material database by clicking the '''Material''' button of &quot;Add Layer&quot; or &quot;Edit Layer&quot; dialogs. This opens the '''Materials''' Dialog. Inside the material list select and highlight any row and click the '''OK''' button. The selected material will fill out all the fields in the &quot;Add Layer&quot; or &quot;Edit Layer&quot; dialogs. Inside the Materials Dialog, you can type the few first letters of any material, and it will take you to the corresponding row of the list.
+=== Transmitter Sweep ===
-[[File:PROP24.png]]
+When your propagation scene contains two or more transmitters, whether they all belong to the same transmitter set with the same radiation pattern or to different transmitter sets, EM.Terrano assumes all to be coherent with respect to one another. In other words, synchronous transmitters are always assumed. The rays originating from all these transmitters are superposed coherently and vectorially at each receiver. In a transmitter sweep, on the other hand, EM.Terrano assumes only one transmitter broadcasting at a time. The result of the sweep simulation is a number of received power coverage maps, each corresponding to a transmitter in the scene.
-Figure: EM.Cube's material list.
+{{Note| EM.Terrano's transmitter sweep works only with the Polarimatrix Solver and requires an existing ray database previously generated using the Channel Analyzer.}}
-=== Transferring Objects From Or To Other Modules ===
+=== Rotational Sweep ===
-When you start a new project in EM.Cube's [[Propagation Module]] and draw a solid object like a box in the project workspace without having defined any surface groups, it is assumed to be of the impenetrable surface type. A default impenetrable surface group called Block_1 is automatically added to the Navigation Tree, which holds your newly drawn object. The default group has the material properties of &quot;Brick&quot; (&epsilon;<sub>r</sub> = 4.4 and &sigma; = 0.001 S/m.) with a dark brown color. You can continue drawing new objects in the project workspace and adding them under this block node. Or you can define a new surface type with different properties. By default, the last surface group that was defined is '''Active'''. The current active surface group is always listed in bold letters in the Navigation Tree. When you draw a new object, it is always inserted under the current active surface group. Any surface group can be activated by right clicking its name in the Navigation Tree and selecting the '''Activate''' item of the contextual menu.
+You can rotate the 3D radiation patterns of both the transmitters and receivers from the property dialog of the parent transmitter set or receiver set. This is done in advance before a SBR simulation starts. You can define one or more of the rotation angles of a transmitter set or a receiver set as sweep variables and perform a parametric sweep simulation. In that case, the entire scene and all of its buildings are discretized at each simulation run and a complete physical SBR ray tracing simulation is carried out. However, we know that the polarimetric characteristics of the propagation channel are independent of the transmitter or receiver antenna patterns or their rotation angles. A rotational sweep allows you to rotate the radiation pattern of the transmitter(s) about one of the three principal axes sequentially. This is equivalent to the steering of the beam of the transmit antenna either mechanically or electronically. The result of the sweep simulation is a number of received power coverage maps, each corresponding to one of the angular samples. To run a rotational sweep, you must specify the rotation angle.
-You can move any object from its current surface group into any other available surface group. First select the object, then right click on its surface and select '''MoveTo &gt; Propagation &gt;'''. A submenu appears which lists all the available surface groups where you can transfer the selected object. You can also move objects among surface groups by selecting their names in the Navigation Tree and using the contextual menu. In a similar way, you can transfer objects from [[Propagation Module]] to EM.Cube's other modules or vice versa. '''Keep in mind that all the external model files such as STEP, IGES, STL, etc. are first imported to EM.Cube's [[CubeCAD]], from which you can transfer them to other modules.''' First select the object, then right click and select '''MoveTo &gt;'''. In the submenu you will see a list of all the EM.Cube modules that have at least one available group where you can transfer your selected object. You can select multiple objects for transfer. When using the keyboard's '''Shift Key''' or '''Ctrl Key''' for multiple selection, make sure that those keys are held down, when you right click to access the contextual menu.
+{{Note| EM.Terrano's rotational sweep works only with the Polarimatrix Solver and requires an existing ray database previously generated using the Channel Analyzer.}}
-== Defining Sources &amp; Observables ==
+=== Mobile Sweep ===
-Like every other electromagnetic solver, EM.Cube's SBR ray tracer requires a source for excitation and one or more observables for generation of simulation data. EM.Cube's new [[Propagation Module]] offers several types of sources and observables for a SBR simulation. You can mix and match different source types and observable types depending on the requirements of your modeling problem. There are two types of sources:
+In a mobile sweep, each transmitter is paired with a receiver according to their indices in their parent sets. At each simulation run, only one (Tx, Rx) pair is considered to be active in the scene. As a result, the generated coverage map takes a different meaning implying the sequential movement of the transmitter and receiver pair along their corresponding paths. In other words, the set of point transmitters and the set of point receivers indeed represent the locations of a single transmitter and a single receiver at different instants of time. It is obvious that the total number of transmitters and total number of receivers in the scene must be equal. Otherwise, EM.Terrano will prompt an error message.
-* [[#Defining Transmitter Sets|Transmitter]]
+[[EM.Cube]] provides a '''Mobile Path Wizard''' that facilitates the creation of a transmitter set or a receiver set along a specified path. This path can be an existing nodal curve (polyline or NURBS curve) or an existing line objects. You can also import a sptial Cartesian data file containing the coordinates of the base location points. For more information, refer to [[Glossary_of_EM.Cube%27s_Wizards#Mobile_Path_Wizard | Mobile Path Wizard]].
-* [[#Hertzian Dipole Sources|Hertzian Dipole]]
-There are four types of observables:
+{{Note| EM.Terrano's mobile sweep works only with the Polarimatrix Solver and requires an existing ray database previously generated using the Channel Analyzer.}}
-* [[#Defining Receiver Sets|Receivers]]
+=== Investigating Propagation Effects Selectively One at a Time ===
-* [[#Defining Field Sensors|Field Sensor]]
-* Far Fields
-* Huygens Surface
-The simplest SBR simulation can be performed using a short dipole source with a specified field sensor plane. In this way, EM.Cube computes the electric and magnetic fields radiated by your dipole source in the presence of your multipath propagation environment. A &quot;classic&quot; urban propagation scene can be set up using a &quot;Transmitter&quot; source and an array of &quot;Receiver&quot; observables. A transmitter is a point radiator with a user defined radiation pattern. A receiver is a polarization-matched isotropic point radiator that collects the received rays at its aperture. Using receivers, you can calculate the received power coverage map of your propagation scene. You can also calculate your channel's path loss between the transmitter and all the receivers. <br />
+In a typical SBR ray tracing simulation, EM.Terrano includes all the propagation effects such as direct (LOS) rays, ray reflection and transmission, and edge diffractions. At the end of a SBR simulation, you can visualize the received power coverage map of your propagation scene, which appears under the receiver set item in the navigation tree. The figure below shows the received power coverage map of the random city scene with a vertically polarized half-wave dipole transmitter located 10m above the ground and a large grid of vertically polarized half-wave dipole receivers placed 1.5m above the ground. The legend box shows the limits of the color map between -23dBm as the maximum and -150dB (the default receiver sensitivity value) as the minimum.
-=== Hertzian Dipole Sources ===
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon10.png|thumb|left|640px|The received power coverage map of the random city scene with a dipole transmitter.]]
+</td>
+</tr>
+</table>
-[[File:PROP18(1).png|thumb|[[Propagation Module]]'s Transmitter dialog with a short dipole radiator selected]]
+Sometime it is helpful to change the scale of the color map to better understand the dynamic range of the coverage map. If you double-click on the legend or right-click on the coverage map's name in the navigation tree and select '''Properties''', the Plot Settings dialog opens up. Select the '''User-Defined''' item and set the lower and upper bounds of color map as you wish.
-Earlier versions of EM.Cube's [[Propagation Module]] used to offer an isotropic radiator with vertical or horizontal polarization as the simplest transmitter type. This release of EM.Cube has abandoned isotropic radiator transmitters because they do not exist physically in a real world. Instead, the default transmitter radiator type is now a Hertzian dipole. Note that before defining a transmitter, first you have to define a base set to establish the location of the transmitter. Most simulation scenes involve only a single transmitter. Your base set can be made up of a single point for this purpose.
-To define a new Transmitter Set, go to the '''Sources''' section of the Navigation Tree, right click on the '''Transmitters''' item and select '''Insert Transmitter...''' A dialog opens up that contains a default name for the new Transmitter Set as well as a dropdown list labeled '''Select Base Set'''. In this list you will see all the available base sets already defined in the project workspace. Select the desired base set to associate with the transmitter set. Note that if the base set contains more than one point, then more than one transmitter will be created and contained in your transmitter set. After defining a transmitter set, the base points change their color to the transmitter color, which is red by default.
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon15.png|thumb|left|480px|The plot settings dialog of the coverage map.]]
+</td>
+</tr>
+</table>
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon16.png|thumb|left|640px|The received power coverage map of the random city scene with a user-defined color map scale between -80dBm and -20dBm.]]
+</td>
+</tr>
+</table>
-In the &quot;Radiator&quot; section of the dialog, you have two options to choose from: &quot;Short Dipole&quot; and &quot;User Defined&quot;. The default option is short dipole. A short dipole radiator has a '''Length'''''dl'' expressed in project units, a current '''Amplitude''' in Amperes and a current '''Phase''' in degrees. The '''Direction''' of the dipole is determined by its unit vector that has three X, Y and Z components. By default, a Z-directed short dipole radiator is assumed. You can change all parameters of the dipole as you wish. Keep in mind that all the transmitters belonging to the same set have parallel radiators with identical properties.
+To better understand the various propagation effects, EM.Terrano allows you to enable or disable these effects selectively. This is done from the Ray Tracing Simulation Engine Settings dialog using the provided check boxes.
-=== Defining Base Point Sets ===
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon14.png|thumb|left|640px|EM.Terrano's simulation run dialog showing the check boxes for controlling various propagation effects.]]
+</td>
+</tr>
+</table>
-[[File:PROP1.png|thumb|[[Propagation Module]]'s Base Set dialog]]
+<table>
-In order to tie up transmitters and receivers with CAD objects in the project workspace, EM.Cube uses point objects to define transmitters and receivers. These point objects represent the base of the location of transmitters and receivers in the computational domain. Hence, they are grouped together as &quot;Base Sets&quot;. You can easily interchange the role of transmitters and receivers in a scene by switching their associated bases. The usefulness of concept of base sets will become apparent later when you place transmitters or receivers on an irregular terrain and adjust their elevation.
+<tr>
+<td>
+[[Image:UrbanCanyon11.png|thumb|left|640px|The received power coverage map of the random city scene with direct LOS rays only.]]
+</td>
+</tr>
+<tr>
+<td>
+[[Image:UrbanCanyon12.png|thumb|left|640px|The received power coverage map of the random city scene with reflected rays only.]]
+</td>
+</tr>
+<tr>
+<td>
+[[Image:UrbanCanyon13.png|thumb|left|640px|The received power coverage map of the random city scene with diffracted rays only.]]
+</td>
+</tr>
+</table>
-To create a new base set, right click on the '''Base Sets''' item of Navigation Tree and select '''Insert Base Set...''' A dialog for setting up the Base Set properties opens up.
+== Working with EM.Terrano's Simulation Data ==
-# Enter a name for the base set and change the default blue color if you wish. It is useful to differentiate the base sets associated with transmitters and receivers by their color.
+=== The Ray Tracing Solvers' Output Simulation Data ===
-# Click the '''OK''' button to close the Base Set Dialog.
-Once a base set node has been added to the Navigation Tree, it becomes the active node for new object drawing. Under base sets, you can only draw point objects. All other object creation tools are disabled. A point is initially drawn on the XY plane. Make sure to change the Z-coordinate of your radiator, otherwise, it will fall on the global ground at z = 0. You can also create arrays of base points under the same base set. This is particularly useful for setting up receiver grids to compute coverage maps. Simply select a point object and click the '''Array Tool''' of '''Tools Toolbar''' or use the keyboard shortcut &quot;A&quot;. Enter values for the X, Y or Z spacing as well as the number of elements along these three directions in the Array Dialog. In most propagation scenes you are interested in 2D horizontal arrays along a fixed Z coordinate (parallel to the XY plane).
+Both the SBR solver and the Polarimatrix solver perform the same type of simulation but in two different ways. The SBR solver discretizes the scene including all the buildings and terrain, shoots a large number of rays from the transmitters and collects the rays at the receivers. The Polarimatrix solver does the same thing using an existing polarimetric ray database that has been previously generated using EM.Terrano's Channel Analyzer. It incorporates the effects of the radiation patterns of the transmit and receive antennas in conjunction with the polarimetric channel characteristics. At the end of a ray tracing simulation, all the polarimetric rays emanating from the transmitter(s) or other sources that are received by the individual receivers are computed, collected, sorted and saved into ASCII data files. From the ray data, the total electric field at the location of receivers as well as the total received power are computed. The individual ray data include the field components of each ray, the ray's elevation and azimuth angles of departure and arrival (departure from the transmitter location and arrival at the receiver location), and time delay of the received ray with respect to the transmitter. If you specify the temperatures, noise figure and transmission line losses in the definition of the receiver sets, the noise power level and signal-to-noise ratio (SNR) at each receiver are also calculated, and so are the E<sub>b</sub>/N<sub>0</sub> and bit error rate (BER) for the selected digital modulation scheme.
-=== Defining Transmitter Sets ===
+=== Visualizing Field & Received Power Coverage Maps ===
-A short dipole is the closest thing to an omni-directional radiator. The direction or orientation of the short dipole determines its polarization. In many applications, you may rather want to use a directional antenna for your transmitter. You can model a radiating structure using EM.Cube's FDTD, Planar, MoM3D or PO modules and generate a 3D radiation pattern data file for it. These data are stored in a specially formatted file with a &quot;'''.RAD'''&quot; extension, which contains columns of spherical &phi; and &theta; angles as well as the real and imaginary parts of the complex-valued far field components '''E<sub>&theta;</sub>''' and '''E<sub>&phi;</sub>'''. The &theta;- and &phi;-components of the far-zone electric field determine the polarization of the transmitting radiator.
+In wireless propagation modeling for communication system applications, the received power at the receiver location is more important than the field distributions. In order to compute the received power, you need three pieces of information:
-To define a directional transmitter radiator, you need to select the &quot;User Defined&quot; option in the &quot;Radiator&quot; section of the Transmitter Dialog. You can do this either at the time of creating a transmitter set, or afterwards by opening the property dialog of the transmitter set. In the &quot;Custom Pattern Parameters&quot;, click the '''Import Pattern''' button to set the path for the radiation data file. This opens up the standard Windows Open dialog, with the default file type or extension set to &quot;.RAD&quot;. Browse your folders to find the right data file. A radiation pattern file usually contains the value of &quot;Total Radiated Power&quot; in its file header. This is used by default for power calculations in the SBR simulation. However, you can check the box labeled &quot;'''Custom Power'''&quot; and enter a value for the transmitter power in Watts. EM.Cube can also rotate the imported radiation pattern arbitrarily. In this case, you need to specify the '''Rotation''' angles in degrees about the X-, Y- and Z-axes. Note that these rotations are performed sequentially and in order: first a rotation about the X-axis, then a rotation about the Y-axis, and finally a rotation about the Z-axis.
+* '''Total Transmitted Power (EIRP)''': This requires knowledge of the baseband signal power, the transmitter chain parameters, the transmission characteristics of the transmission line connecting the transmitter circuit to the transmitting antenna and the radiation characteristics of the transmitting antenna.
+* '''Channel Path Loss''': This is computed through SBR simulation.
+* '''Receiver Properties''': This includes the radiation characteristics of the receiving antenna, the transmission characteristics of the transmission line connecting the receiving antenna to the receiver circuit and the receiver chain parameters.
-[[File:PROP19(1).png]] [[File:PROP20(1).png]]
+In a simple link scenario, the received power P<sub>r</sub> in dBm is found from the following equation:
-Figure 1: [[Propagation Module]]'s Transmitter dialog with a user defined radiator selected.
+<math> P_r [dBm] = P_t [dBm] + G_{TC} + G_{TA} - PL + G_{RA} + G_{RC} </math>
-=== Multiple Transmitters vs. Antenna Arrays ===
+where P<sub>t</sub> is the baseband signal power in dBm at the transmitter, G<sub>TC</sub> and G<sub>RC</sub> are the total transmitter and receiver chain gains in dB, respectively, G<sub>TA</sub> and G<sub>RA</sub> are the total transmitting and receiving antenna gains in dB, respectively, and PL is the channel path loss in dB. Keep in mind that EM.Terrano is fully polarimetric. The transmitting and receiving antenna characteristics are specified through the imported radiation pattern files, which are part of the definition of the transmitters and receivers. In particular, the polarization mismatch losses are taken into account through the polarimetric SBR ray tracing analysis.
-EM.Cube's SBR simulations are fully coherent and 3D-polarimetric. This means that the phase and polarization of all the rays are maintained and processed during their bounces in the scene. Your propagation scene can have more than one transmitter. During an SBR simulation, all the rays emanating from all the transmitters are traced in the propagation scene. All the received rays at a given receiver location are summed coherently and vectorially. This is based on the principle of linear superposition. All the transmitters belonging to the same transmitter set have the same radiation properties. They are either parallel short dipole radiators with the same current amplitudes and phases, or parallel user defined radiators with identical radiation patterns. As these transmitters are placed at different spatial locations, they effectively form an antenna array with identical elements. The array factor is simply determined by the coordinates of the base points. If you want to have different amplitude or phases, then you need to define different transmitter sets.
+If you specify the noise-related parameters of your receiver set, the signal-to-noise ratios (SNR) is calculated at each receiver location: SNR = P<sub>r</sub> - P<sub>n</sub>, where P<sub>n</sub> is the noise power level in dB. When planning, designing and deploying a communication system between points A and B, the link is considered to be closes and a connection established if the received signal power at the location of the receiver is above the noise power level by a certain threshold. In other words, the SNR at the receiver must be greater than a certain specified minimum SNR level. You specify (SNR)<sub>min</sub> ss part of the definition of receiver chain in the Receiver Set dialog. In the "Visualization Options" section of this dialog, you can also check the check box labeled '''Generate Connectivity Map'''. This is a binary-level black-and-white map that displays connected receivers in white and disconnected receivers in black. At the end of an SBR simulation, the computed SNR is displayed in the Receiver Set dialog for the selected receiver. The connectivity map is generated and added to the navigation tree underneath the received power coverage map node.
-If that radiators are indeed the elements of an actual antenna array with a half wavelength spacing or so, we recommend that you import the radiation pattern of the array structure instead and replace the whole multi-radiator system with a single point transmitting radiator in your propagation scene. This case is usually encountered in MIMO systems, and using an equivalent point transmitter is an acceptable approximation because the total size of the array aperture is usually much smaller than the dimensions of your propagation scene and its representative length scales. In that case, you need to position the equivalent point radiator at the radiation center of the antenna array. This depends on the physical structure of the antenna array. However, keep in mind that any reasonable guess may still provide a good approximation without any significant error in the received ray data.
+At the end of an SBR simulation, you can visualize the field maps and receiver power coverage map of your receiver sets. A coverage map shows the total '''Received Power''' by each of the receivers and is visualized as a color-coded intensity plot. Under each receiver set node in the navigation tree, a total of seven field maps together with a received power coverage map are added. The field maps include amplitude and phase plots for the three X, Y, Z field components plus a total electric field plot. To display a field or coverage map, simply click on its entry in the navigation tree. The 3D plot appears in the Main Window overlaid on your propagation scene. A legend box on the right shows the color scale and units (dB). The 3D coverage maps are displayed as horizontal confetti above the receivers. You can change the appearance of the receivers and maps from the property dialog of the receiver set. You can further customize the settings of the 3D field and coverage plots.
-=== Defining Receiver Sets ===
+<table>
+<tr>
+<td>
+[[Image:AnnArbor Scene1.png|thumb|left|640px|The downtown Ann Arbor propagation scene.]]
+</td>
+</tr>
+<tr>
+<td>
+[[Image:AnnArbor Scene2.png|thumb|left|640px|The electric field distribution map of the Ann Arbor scene with vertical dipole transmitter and receivers.]]
+</td>
+</tr>
+<tr>
+<td>
+[[Image:AnnArbor Scene3.png|thumb|left|640px|The received power coverage map of the Ann Arbor scene with vertical dipole transmitter and receivers.]]
+</td>
+</tr>
+<tr>
+<td>
+[[Image:AnnArbor Scene4.png|thumb|left| 640px |The connectivity map of the Ann Arbor scene with SNR<sub>min</sub> = 3dB with the basic color map option.]]
+</td>
+</tr>
+<tr>
+<td>
+[[Image:AnnArbor Scene5.png|thumb|left| 640px |The connectivity map of the Ann Arbor scene with SNR<sub>min</sub> = 20dB with the basic color map option.]]
+</td>
+</tr>
+</table>
-Receivers act as observables in a propagation scene. The objective of a SBR simulation is to calculate the far-zone electric fields and the total received power at the location of a receiver. In that sense, receivers indeed act as field observation points. You need to define at least one receiver in the scene before you can run a SBR simulation. You define the receivers of your scene by associating them with the base sets you have already defined in the project workspace. Unlike transmitters that usually one or few, a typical propagation scene may involve a large number of receivers. To generate a wireless coverage map, you need to define an array of points as your base set.
+=== Visualizing the Rays in the Scene ===
-To define a new Receiver Set, go to the Observables section of the Navigation Tree, right click on the '''Receivers''' item and select '''Insert Receiver...''' A dialog opens up that contains a default name for the new Receiver Set as well as a dropdown list labeled '''Select Radiator Set'''. In this list you will see all the available base sets that you have already define in the project workspace. Select and designate the desired base set as the receiver set. Note that if the base set contains more than one point, all of them are designated as receivers. After defining a receiver set, the points change their color to the receiver color, which is yellow by default. The first element of the set is represented by a larger ball of the same color indicating that it is the selected receiver in the scene. The Receiver Set Dialog is also used to access individual receivers of the set for data visualization at the end of a simulation. At the end of an SBR simulation, the button labeled &quot;Show Ray Data&quot; becomes enabled. Clicking this button opens the Ray Data Dialog, where you can see a list of all the received rays at the selected receiver and their computed characteristics.
-[[File:PROP21(1).png]] [[File:PROP22.png]]
-Figure 1: [[Propagation Module]]'s Receiver dialog.
-=== Defining Field Sensors ===
-[[File:PMOM90.png|thumb|[[Propagation Module]]'s Field Sensor dialog]]
-As an asymptotic electromagnetic field solver, the SBR simulation engine can compute the electric and magnetic field distributions in a specified plane. In order to view these field distributions, you must first define field sensor observables before running the SBR simulation. To do that, right click on the '''Field Sensors''' item in the '''Observables''' section of the Navigation Tree and select '''Insert New Observable...'''. The Field Sensor Dialog opens up. At the top of the dialog and in the section titled '''Sensor Plane Location''', first you need to set the plane of field calculation. In the dropdown box labeled '''Direction''', you have three options X, Y, and Z, representing the&quot;normals&quot; to the XY, YZ and ZX planes, respectively. The default direction is Z, i.e. XY plane parallel to the substrate layers. In the three boxes labeled '''Coordinates''', you set the coordinates of the center of the plane. Then, you specify the '''Size''' of the plane in project units, and finally set the '''Number of Samples''' along the two sides of the sensor plane. The larger the number of samples, the smoother the near field map will appear.
-In the section titled Output Settings, you can also select the field map type from two options: '''Confetti''' and '''Cone'''. The former produces an intensity plot for field amplitude and phase, while the latter generates a 3D vector plot. In the confetti case, you have an option to check the box labeled '''Data Interpolation''', which creates a smooth and blended (digitally filtered) map. In the cone case, you can set the size of the vector cones that represent the field direction. At the end of a sweep simulation, multiple field map are produced and added to the Navigation Tree. You can animate these maps. However, during the sweep only one field type is stored, either the E-field or H-field. You can choose the field type for multiple plots using the radio buttons in the section titled '''Field Display - Multiple Plots'''. The default choice is the E-field.
-Once you close the Field Sensor dialog, its name is added under the '''Field Sensors''' node of the Navigation Tree. At the end of a SBR simulation, the field sensor nodes in the Navigation Tree become populated by the magnitude and phase plots of the three vectorial components of the electric ('''E''') and magnetic ('''H''') field as well as the total electric and magnetic fields defined in the following manner:
-:<math> \mathbf{|E_{tot}|} = \sqrt{|E_x|^2 + |E_y|^2 + |E_z|^2} </math>
-:<math> \mathbf{|H_{tot}|} = \sqrt{|H_x|^2 + |H_y|^2 + |H_z|^2} </math>
-<!--[[File:PMOM88.png]]-->
-=== Computing Radiation Patterns In SBR ===
-Coming Soon...
-== Scene Discretization &amp; Adjustment ==
-=== The Need For Discretization Of Propagation Scene ===
-In a typical SBR simulation, a ray is traced from the location of the source until it hits a scatterer. The SBR method assumes that the ray hits either a flat facet of the scatterer or one of its edges. In the case of hitting a flat facet, the specular point is used to launch new reflected and transmitted rays. The surface of the facet is treated as an infinite dielectric medium interface, at which the reflection and transmission coefficients are calculated. In the case of hitting an edge, new diffracted rays are generated in the scene. However, only those who reach a nearby receiver in their line of sight are ever taken into account. In other words, diffractions are treated locally.
-EM.Cube's [[Propagation Module]] allows you to draw any type of surface or solid CAD objects under impenetrable and penetrable surface groups. Some of these objects have flat faces such as boxes, pyramids, rectangle or triangle strips, etc. Some others contain curved surfaces or curved boundaries such as cylinders, cones, etc. All the non-flat surfaces have to be discretized in the form of a collection of smaller flat facets. EM.Cube uses a triangular surface mesh generator to discretize the penetrable and impenetrable [[Surface Objects|surface objects]] of your propagation scene. This mesh generator is very similar to the ones used in EM.Cube's two other modules: MoM3D and Physical Optics (PO).
-You can build a variety of surface and [[Solid Objects|solid objects]] using EM.Cube's native &quot;Curve&quot; CAD objects like lines, polylines, circles, etc. You can use tools like Extrude, Loft, Strip-Sweep, Pipe-Sweep, etc. to transform curves into surface or [[Solid Objects|solid objects]]. '''However, keep in mind that all the &quot;Curve&quot; CAD objects are ignored by the SBR mesh generator and are therefore not sent to the simulation engine.'''
-=== Viewing SBR Mesh ===
-You can view and examine the discretized version of your scene objects as they are sent to the SBR simulation engine. To view the mesh, click the '''Mesh''' [[File:mesh_tool.png]] button of the Simulate Toolbar or select '''Simulate &gt; Discretization &gt; Show Mesh''', or use the keyboard shortcut '''Ctrl+M'''. A triangular surface mesh of your physical structure appears in the project workspace. In this case, EM.Cube enters it mesh view mode. You can perform view operations like rotate view, pan, zoom, etc. But you cannot select objects, or move them or edit their properties. To get out of the Mesh View and return to EM.Cube's Normal View, press the '''Esc Key''' of the keyboard, or click the Mesh button of the Simulate Toolbar once again, or go to the Simulate Menu and deselect the '''Discretization &gt;''' '''Show Mesh''' item.
-You can adjust the mesh resolution and increase the geometric fidelity of discretization by creating more and finer triangular facets. On the other hand, you may want to reduce the mesh complexity and send to the SBR engine only a few coarse facets to model your buildings. To adjust the mesh resolution, open the Mesh Settings Dialog by clicking the '''Mesh Settings''' [[File:mesh_settings.png]] button of the Simulate Toolbar or select '''Simulate &gt; Discretization &gt;''' '''Mesh Settings...'''. This dialog provides a single parameters: '''Edge Length'''., which has a default value of 100 project units. If you are already in the Mesh View Mode and open the Mesh Settings Dialog, you can see the effect of changing the edge length using the '''Apply''' button. Click OK to close the dialog.
-Note that unlike EM.Cube's other computational modules that express the default mesh density based on the wavelength, the resolution of the SBR mesh generator is expressed in project length units. The default edge length value of 100 units might be too large for non-flat objects. You may have to use a lower value to capture the curvature of your curved structures adequately.
-[[File:prop_manual-29.png]]
-Figure 1: [[Propagation Module]]'s Mesh Settings dialog.
-=== Special Discretized Object Types ===
-In EM.Cube, terrain objects are represented by and saved as special &quot;Tessellated&quot; objects with quadrilateral cells. This is true of terrain objects that you create yourself using EM.Cube's Terrain Generator as well as all the terrain objects that you import from external files to your project. The center of each cell represents the terrain elevation at that point. Tessellated objects are considered as discretized objects by EM.Cube and they are not meshed one more time by the SBR mesh generator. Each quadrilateral cell is divided into two triangular cells before being passed to the SBR simulation engine. Therefore, when using EM.Cube's Terrain Generator to create a new terrain object, you have to pay special attention to the resolution of the terrain object as it determines the total number of terrain facets sent to the simulation engine. A high resolution terrain, although looking better and more realistic, may easily lead to an enormous computational problem.
-You can use EM.Cube's &quot;Polymesh&quot; tool to discretize solid and surface CAD objects. You can manually control the mesh characteristics of polymesh objects including inserting new nodes on faces and edges or deleting existing nodes. In addition, EM.Cube's Solid Generator and Surface Generator tools create ploymesh solids and surfaces, respectively. Like tessellated object, polymesh objects are also considered as discretized objects by EM.Cube and they are not meshed again by the SBR mesh generator.
-=== SBR Mesh Rules &amp; Considerations ===
-Coming Soon...
-=== Adjusting Block Elevation On Terrain ===
-In EM.Cube, buildings and all other CAD objects are initially created on the XY plane by default. In other words, the Z-coordinate of the local coordinate system (LCS) of all blocks is set to zero until you change them. As long as you use the global ground, all is fine as your buildings are seated on the ground. When your propagation scene has an irregular terrain, you want to place your buildings on the terrain and not buried under it. Buildings in EM.Cube are not adjusted to the terrain elevation automatically. You need to instruct EM.Cube to do so.
-To update the building positions and adjust their elevation to the underlying terrain, right click on the '''Terrain''' item of the Navigation Tree and select '''Adjust Scene Elevation''' from the context menu. All the blocks in the scene are automatically elevated in the Z direction such that their bases sit on the terrain. In effect, all the blocks are translated along the global Z axis by proper amounts such that their local Z coordinate equals the Z-elevation of the underlying terrain object. This feature is particularly useful if you change the location of the terrain or import a new terrain after the blocks have been created.
-Note: You have to make sure that the resolution of your terrain, its fluctuation scale and building dimensions are all comparable. Otherwise, on a high-resolution, rapidly varying terrain, you will have buildings whose bottoms are in contact with the terrain only at a few points and parts of them hang in the air.
-[[File:prop_adjust1_tn.png|400px]] [[File:prop_adjust2_tn.png|400px]]
-Figure: A Scene with Buildings and Terrain Before and After Adjusting Elevation
-=== Transmitters &amp; Receivers Above An Irregular Terrain ===
-In EM.Cube, all the transmitters and receivers are tied up with point objects in the project workspace. These point objects are grouped and organized in base sets. When you move the point objects or change their coordinates, all of their associated transmitters or receivers immediately follow them to the new location. For example, you usually define a grid of receivers using a base set that is made up of a uniformly spaced array of points and spread them in your scene. All of these receivers have the same height because their associated base points all have the same Z-coordinate. When your receivers are located above a flat terrain like the global ground, their Z-coordinates are equal to their height above the ground, as the terrain elevation is fixed and equal to zero everywhere. The same is true for transmitters, too.
-In many propagation modeling problems, your transmitters and receivers may be located above an irregular terrain with varying elevation across the scene. In that case, you may want to place your transmitters or receivers at a certain height above the underlying ground. The Z-coordinate of a transmitter or receiver is now the sum of the terrain elevation at the base point and the specified height. EM.Cube gives you the option to adjust the transmitter and receiver sets to the terrain elevation. This is done for individual transmitter sets and individual receiver sets. At the top of the Transmitter Dialog there is a check box labeled &quot;'''Adjust Tx Sets to Terrain Elevation'''&quot;. Similarly, at the top of the Receiver Dialog there is a check box labeled &quot;'''Adjust Rx Sets to Terrain Elevation'''&quot;. These boxes are unchecked by default. As a result, your transmitter sets or receiver sets coincide with their associated base points in the project workspace. If you check these boxes and place a transmitter set or a receiver set above an irregular terrain, the transmitters or receivers are elevated from the location of their associated base points by the amount of terrain elevation as can be seen in the figure below.
-To better understand why there are two separate sets of points in the scene, note that a point array (CAD object) is used to create a uniformly spaced base set. The array object always preserves its grid topology as you move it around the scene. However, the transmitters or receivers associated with this point array object are elevated above the irregular terrain and no longer follow a strictly uniform grid. If you move the base set from its original position to a new location, the base points' topology will stay intact, while the associated transmitters or receivers will be redistributed above the terrain based on their new elevations.
-[[File:prop_txrx1_tn.png|400px]] [[File:prop_txrx2_tn.png|400px]]
-Figure: Transmitters and receivers adjusted above an uneven terrain and their associated base sets.
-== Running A SBR Simulation ==
-EM.Cube's [[Propagation Module]] offers three types of ray tracing simulations:
-* Analysis
-* Frequency Sweep
-* Parametric Sweep
-An SBR analysis is the simplest ray tracing simulation and involves the following steps:
-# Set the unit of project scene and the frequency of operation. Note that EM.Cube's default project unit is millimeter. When working with the [[Propagation Module]], pay attention to the project unit. Radio propagation problems usually require meter, mile or kilometer as the project unit.
-# Create the blocks and draw the buildings at the desired locations.
-# Keep the default ray domain and accept the default global ground or change its material properties.
-# Define the base sets (at least one for the transmitter and one for the receiver).
-# Define the transmitter and receiver(s) using the available base sets.
-# Run the SBR simulation engine.
-# Visualize the coverage map and plot other data.
-You can access the [[Propagation Module]]'s run dialog by clicking the '''Run''' [[File:run_icon.png]] button of the '''Simulate Toolbar''' or by selecting '''Simulate &gt; Run...''' or using the keyboard shortcut '''Ctrl+R'''. When you click the '''Run''' button, a new window opens up that reports the different stages of the SBR simulation and indicates the progress of each stage. After the SBR simulation is successfully completed, a message pops up and prompts the completion of the process.
-[[File:PROP12.png]]
-Figure 1: [[Propagation Module]]'s Simulation Run dialog.
-=== SBR Simulation Parameters ===
-There are a number of SBR simulation settings that can be accessed and changed from the SBR Settings Dialog. To open this dialog, click the button labeled '''Settings''' on the right side of the '''Select Engine''' dropdown list in the Run Dialog. EM.Cube's SBR simulation engine allows you to separate the physical effects that are calculated during a ray tracing process. You can selectively enable or disable '''Ray Reflection''', '''Ray Transmission''' and '''Ray Diffraction'''. By default, all three effects are checked and included in the computations. Separating these effects sometimes help you better analyze your propagation scene and understand the impact of various blocks in the scene.
-EM.Cube requires a finite number of ray bounces for each original ray emanating from a transmitter. This is very important in situations that may involve resonance effects where rays get trapped among certain group of surfaces and may bounce back and forth indefinitely. This is set using the box labeled &quot;'''Max No. Ray Bounces'''&quot;, which has a default value of 10. Note that the maximum number of ray bounces directly affects the computation time as well as the size of output simulation data files. This can become critical for indoor propagation scenes, where most of the rays undergo a large number of reflections.
-As rays travel in the scene and bounce from surfaces, they lose their power and their amplitudes diminish. From a practical point of view, only rays that have power above the receiver sensitivity threshold can be effectively received. Therefore, all the rays whose power fall below a specified power threshold are discarded. The '''Ray Power Threshold''' is specified in dBm and has a default value of -100dBm. Keep in mind that the value of this threshold directly affects the accuracy of the simulation results as well as the size of the output data file.
-You can also set the '''Angular Resolution''' of the transmitter rays in degrees. By default, every transmitter emanates equi-angular ray tubes at a resolution of 1 degree. Lower angular resolutions larger than 1° speed up the SBR simulation significantly, but they may compromise the accuracy. Higher angular resolutions less than 1° increase the accuracy of the simulating results, but they also increase the computation time.
-[[File:PROP13.png]]
-Figure 1: [[Propagation Module]]'s SBR Engine Settings dialog.
-=== The Coverage Map ===
-If the associated radiator set is isotropic, so will be the transmitter set. By default, an isotropic transmitter has vertical polarization. You can use the '''Polarization''' radio button to select one of the two options: '''Vertical''' or '''Horizontal'''. If the associated radiator set consists of '''Short Dipole''' or '''User Defined''' radiators, it is indicated in the transmitter property dialog. In the case of a short dipole radiator, you can set a value for the dipole current in Amperes. The radiation resistance of a short dipole of length ''dl'' is given by:
-:<math> R_r = 80\pi^2 \left( \frac{dl}{\lambda_0} \right)^2 </math>
-<!--[[File:eqngr6.png]]-->
-The radiated power of a short dipole carrying a current I<sub>0</sub> is then given by:
-:<math> P_{rad} = \frac{1}{2} R_r |I_0|^2 = 40\pi^2 |I_0|^2 \left( \frac{dl}{\lambda_0} \right)^2 </math>
-<!--[[File:shortdipole.png]]-->
-For isotropic and user defined radiators you can set the '''Input Power''' and '''Phase''' of a transmitter set in Watts and degrees, respectively. This can be accessed from the '''Transmitter Chain''' dialog, which will be described in detail in the next section. The radiation pattern of the associated radiator set is normalized and used in conjunction with the input power value to create a weighted distribution of transmitted rays. In certain cases like hybrid simulations, you may want to use the actual values of the far field to define the transmitter power rather than a normalized radiation pattern. Note that the pattern (.RAD) file contains the value of total radiated power in its header. In this case, check the box labeled '''&quot;Calculate Power From Radiation Pattern&quot;'''. This is calculated directly from the complex &theta; and &phi; components of the far field data by integrating them over the entire space (4&pi; solid angle). Note that this option is available only when the radiator is of the User Defined type. When this box is checked, the transmitter chain button is grayed out. By default, an isotropic transmitter emanates rays uniformly in all directions at the angular resolution specified by the user. A transmitter with a user defined associated radiator may represent a highly directional radiation pattern with the main beam pointing in a certain direction. You can additionally force and limit the '''Angular Extents''' of rays to a certain solid angle around the transmitter. This is especially useful and computationally efficient when the transmitter is on one side of the scene, and all the scatterers and receivers are on the other side. In this case, there is no need to generate rays in all directions. To limit the angular extents of rays, define the Start and End values for both Theta (&theta;) and Phi (&phi;) angles. The value of the angular resolution of the rays can be changed from the Run Dialog as will be discussed later.
-In a regular SBR simulation, you have a transmitter and one or more arrays of receivers in your scene. At the end of the simulation, you can visualize the coverage map of the transmitter over the receiver sets. A coverage map shows the total '''Received Power''' by each of the receivers and is visualized as a color-coded intensity plot. You can visualize the coverage maps of individual receiver sets. At the end of a SBR simulation, each Received Power Coverage Map is listed under the receiver set's name in the Navigation Tree. To display a coverage map, simply click on its entry in the Navigation Tree. The coverage map plot appears in the Main Window overlaid on the scene. A legend box on the right shows the color scale and units (dB). The 3-D coverage maps are displayed as horizontal confetti above the receivers. If the receivers are packed close to each other, you will see a continuous confetti map. If the receivers are far apart, you will see individual colored squares. You can also visualize coverage maps as colored 3-D cubes. This may be useful when you set up your receivers in a vertical arrangement or the scene has a highly uneven terrain. To change the type of coverage map visualization, open the receiver set's property dialog and select the desired option for '''Coverage Map: Confetti''' or '''Cube''' in the '''&quot;Visualization Options&quot;''' section of the dialog.
-[[File:prop_run11_tn.png|400px]] [[File:prop_run12_tn.png|400px]]
-Figure: Received power coverage map: (Left) confetti style, and (Right) cube style.
-You can change the settings of the coverage map by right clicking on its entry in the Navigation Tree and selecting '''Properties...''' or by double-clicking on the legend box. In the Output Plot Settings dialog, you can choose from one of three Color Map options: '''Default''', '''Rainbow''' and '''Grayscale'''. The visualization plot uses default values for the color scale. In the section titled &quot;Limits&quot;, you can choose the radio button labeled '''User Defined'''. Then, you have to enter new values for the '''Lower''' and '''Upper''' Limits of the plot. You can also show or hide the Legend Box or change its '''Background''' and '''Foreground''' colors by clicking the buttons provided for this purpose.
-[[File:prop_run4.png]]
-Output Plot Settings
-=== The Ray Data ===
 At the end of a SBR simulation, each receiver receives a number of rays. Some receivers may not receive any rays at all. You can visualize all the rays received by a certain receiver from the active transmitter of the scene. To do this, right click the '''Receivers''' item of the Navigation Tree. From the context menu select '''Show Received Rays'''. All the rays received by the currently selected receiver of the scene are displayed in the scene. The rays are identified by labels, are ordered by their power and have different colors for better visualization. You can display the rays for only one receiver at a time. The receiver set property dialog has a list of all the individual receivers belonging to that set. To display the rays received by another receiver, you have to change the '''Selected Receiver''' in the receiver set's property dialog. If you keep the mouse focus on this dropdown list and roll your mouse scroll wheel, you can scan the selected receivers and move the rays from one receiver to the next in the list. To remove the visualized rays from the scene, right click the Receivers item of the Navigation Tree again and from the context menu select '''Hide Received Rays'''.
-[[File:prop_run5_tn.png|800px]]
-Visualization of received rays at the location of the selected receiver.
 You can also view the ray parameters by opening the property dialog of a receiver set. By default, the first receiver of the set is always selected. You can select any other receiver from the drop-down list labeled '''Selected Receiver'''. If you click the button labeled '''Show Ray Data''', a new dialog opens up with a table that contains all the received rays at the selected receiver and their parameters:
@@ Line 699: / Line 877: @@
 * Ray Power is the received power at the receiver due to a specific ray and is given in dBm.
 * Angles of Arrival are the &theta; and &phi; angles of the incoming ray at the local spherical coordinate system of the receiver.
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon17.png|thumb|left|720px|EM.Terrano's ray data dialog showing a selected ray.]]
+</td>
+</tr>
+</table>
 The Ray Data Dialog also shows the '''Total Received Power''' in dBm and '''Total Received Field''' in dBV/m due to all the rays received by the receiver. You can sort the rays based on their delay, field, power, etc. To do so, simply click on the grey column label in the table to sort the rays in ascending order based on the selected parameter. You can also select any ray by clicking on its '''ID''' and highlighting its row in the table. In that case, the selected rays is highlighted in the Project Workspace and all the other rays become thin (faded).
-Note: The rays are summed up coherently at the receiver.
+{{Note|All the received rays are summed up coherently in a vectorial manner at the receiver location.}}
-[[File:prop_run6_tn.png|800px]]
+<table>
+<tr>
+<td> [[Image:UrbanCanyon18.png|thumb|left|640px|Visualization of received rays at the location of a selected receiver in the random city scene.]] </td>
+</tr>
+</table>
-Figure: Analyzing a selected ray from the ray data dialog.
+=== The Standard Output Data File ===
-=== Plotting Other Simulation Results ===
-Besides visualizing the coverage map and received rays in the EM.CUBE's [[Propagation Module]], you can also plot the '''Path Loss''' of all the receivers belonging to a receiver set as well as the '''Power Delay Profile''' of individual receivers. To plot these data, go the '''Observables''' section of the Navigation Tree and right click on the '''Receivers''' item. From the context menu, select '''Plot Path Loss''' or '''Plot Power Delay Profile''', respectively. The path loss data between the active transmitter and all the receivers belonging to a receiver set are plotted on a Cartesian graph. The horizontal axis of this graph represents the index of the receiver. Power Delay Profile is a bar chart that plots the power of individual rays received by the currently selected receiver versus their time delay. If there is a line of sight (LOS) between a transmitter and receiver, the LOS ray will have the smallest delay and therefore will appear first in the bar chart. Sometimes you may have several rays arriving at a receiver at the same time, i.e. all with the same delay, but with different power level. These will appear as stacked bars in the chart.
-You can also plot the path loss and power delay profile graphs and many others from EM.CUBE's data manager. You can open data manager by clicking the '''Data Manager''' [[File:data_manager_icon.png]] button of the '''Compute Toolbar''' or by selecting '''Compute [[File:larrow_tn.png]] Data Manager''' from the menu bar or by right clicking on the '''Data Manager''' item of the Navigation Tree and selecting Open Data Manager... from the contextual menu or by using the keyboard shortcut '''Ctrl+D'''. In the Data manager Dialog, you will see a list of all the data files available for plotting. These include the theta and phi angles of arrival and departure of the selected receiver. You can select any data file by clicking and highlighting its '''ID''' in the table and then clicking the '''Plot''' button.
-=== Output Data Files ===
+At the end of an SBR simulation, EM.Terrano writes a number of ASCII data files to your project folder. The main output data file is called "sbr_results.RTOUT". This file contains all the information about individual receivers and the parameters of each ray that is received by each individual receiver.
 At the end of an SBR simulation, the results are written into a main output data file with the reserved name of SBR_Results.RTOUT. This file has the following format:
-NEW LINE:
+Each receiver line has the following information:
-* Receiver Number
+* Receiver ID
-* Receiver Base X, Y , Z Coordinates
+* Receiver X, Y, Z coordinates
-* Receiver Height
+* Total received power in dBm
+* Total number of received rays
-NEW LINE:
+Each rays line received by a receiver has the following information:
-Number of Rays
+* Ray Index
+* Delay in nsec
-NEW LINE:
-* Ray Number
 * &theta; and &phi; Angles of Arrival in deg
 * &theta; and &phi; Angles of Departure in deg
-* Delay in nsec
+* Real and imaginary parts of the three E<sub>x</sub>, E<sub>y</sub>, E<sub>z</sub> components
-* Real(E<sup>V</sup>) &amp; Imag(E<sup>V</sup>)
+* Number of ray hit points
-* Real(E<sup>H</sup>) &amp; Imag(E<sup>H</sup>)
+* Coordinates of individual hit points
-* Real('''E.e<sub>R</sub>''') &amp; Imag('''E.e<sub>R</sub>''')
-* Power
-The angles of arrival are the &theta; and &phi; angles of a received ray measured in degrees and are referenced in the spherical coordinate systems centered at the location of the receiver. The angles of departure for a received ray are the &theta; and &phi; angles of the originating transmitter ray, measured in degrees and referenced in the spherical coordinate systems centered at the location of the active transmitter, which eventually arrives at the receiver. The total time delay is measured in nanoseconds between t = 0 nsec at the time of launch from the transmitter location till being received at the receiver location. The last four columns show the real and imaginary parts of the received electric fields with vertical and horizontal polarizations, respectively. The complex field values are normalized in a way that when their magnitude is squared, it equals the received ray power. If the active transmitter is an isotropic radiator with either a vertical or horizontal polarization, then the field components corresponding to the other polarization will have zero entries in the output data file.
+The angles of arrival are the &theta; and &phi; angles of a received ray measured in degrees and are referenced in the local spherical coordinate systems centered at the location of the receiver. The angles of departure for a received ray are the &theta; and &phi; angles of the originating transmitter ray, measured in degrees and referenced in the local spherical coordinate systems centered at the location of the active transmitter, which eventually arrives at the receiver. The total time delay is measured in nanoseconds between t = 0 nsec at the time of launch from the transmitter location till being received at the receiver location.
-[[File:prop_run8_tn.png|800px]]
+<table>
+<tr>
+<td>
+[[Image:prop_run8_tn.png|thumb|left|720px|A typical SBR output data file.]]
+</td>
+</tr>
+</table>
-Figure: A typical SBR output data file.
+=== Plotting Other Simulation Results ===
-=== Running A Frequency Sweep With SBR ===
+Besides "sbr_results.out", [[EM.Terrano]] writes a number of other ASCII data files to your project folder. You can view or plot these data in [[EM.Cube]]'s Data Manager. You can open data manager by clicking the '''Data Manager''' [[File:data_manager_icon.png]] button of the '''Simulate Toolbar''' or by selecting '''Menu > Simulate > Data Manager''' from the menu bar or by right-clicking on the '''Data Manager''' item of the navigation tree and selecting '''Open Data Manager...''' from the contextual menu or by using the keyboard shortcut {{key|Ctrl+D}}.
-By default, you run a single-frequency simulation in EM.CUBE's [[Propagation Module]]. You set the operational frequency of a SBR simulation in the project's '''Frequency Dialog''', which can be accessed in a number of ways:
+The available data files in the "2D Data Files" tab of Data Manger include:
-# By clicking the '''Frequency''' [[File:freq_icon.png]] button of the '''Compute Toolbar'''.
+* '''Path Loss''': The channel path loss is defined as PL = P<sub>r</sub> - EIRP. The path loss data are stored in a file called "SBR_receiver_set_name_PATHLOSS.DAT" as a function of the receiver index. The path loss data make sense only if your receiver set has the default isotropic radiator.
-# By selecting '''Compute''' [[File:larrow_tn.png]]'''Frequency Settings...''' from the Menu Bar.
+* '''Power Delay Profile''': The delays of the individual rays received by the selected receiver with respect to the transmitter are expressed in ns and tabulated together with the power of each ray in the file "SBR_receiver_set_name_DELAY.DAT". You can plot these data from the Data Manager as a bar chart called the power delay profile. The bars indeed correspond to the difference between the ray power in dBm and the minimum power threshold level in dBm, which makes them a positive quantity.
-# Using the keyboard shortcut '''Ctrl+F'''.
+* '''Angles of Arrival''': These are the Theta and Phi angles of the individual rays received by the selected receiver and saved to the files "SBR_receiver_set_name_ThetaARRIVAL.ANG" and "SBR_receiver_set_name_PhiARRIVAL.ANG". You can plot them in the Data Manager in polar stem charts.
-# By double clicking the frequency section (box) of the '''Status Bar'''.<br />
-[[File:prop_freq.png]]    [[File:prop_run10.png]]
+When you run a frequency or parametric sweep in [[EM.Terrano]], a tremendous amount of data may be generated. [[EM.Terrano]] only stores the '''Received Power''', '''Path Loss''' and '''SNR''' of the selected receiver
+in ASCII data files called "PREC_i.DAT", "PL_i.DAT" and "SNR_i.DAT", where is the index of the receiver set in your scene. These quantities are tabulated vs. the sweep variable's samples. You can plot these files in EM.Grid.
-(Left) Project's frequency dialog and (Right) the frequency settings dialog.
+[[Image:Info_icon.png|40px]] Click here to learn more about working with data filed and plotting graphs in [[EM.Cube]]'s '''[[Defining_Project_Observables_%26_Visualizing_Output_Data#The_Data_Manager | Data Manager]]'''.
-You can also select the '''Frequency Sweep''' option in the '''Simulation Mode''' drop-down list of the '''Run Dialog'''. Click the '''Settings...''' button on the right side of this dropdown list to open up the Frequency Settings Dialog. Based on the original values of the project center frequency and bandwidth, the '''Start Frequency''' and '''End Frequency''' have default values. You can also change the '''Number of Samples'''. Once you click the '''Run''' button, EM.CUBE performs a frequency sweep by assigning each of the frequency samples as the current operational frequency and running the SBR simulation engine at that frequency. All the simulation data at all frequency samples are saved into the output data files including &quot;SBR_results.RTOUT&quot;. After the completion of a frequency sweep simulation, as many coverage maps as the number of frequency samples are generated and added to the Navigation Tree under the Receiver Set's entry. You can click on each of the coverage maps corresponding to each of the frequency samples and visualize it in the project workspace. You can also animate the coverage maps. To do so, right click on the receiver set's name in the Navigation Tree and select '''Animation''' from the contextual menu. The coverage maps start to animate by their order on the Navigation Tree. Once the entire list is displayed sequentially, it starts all over again from the beginning of the list. During the animation, the '''Animation Controls''' dialog appears at the lower right corner of the screen. This dialog has a number of buttons for pause/resume, step forward/backward, and step to the end/start. The title of each coverage map is shown in the box labeled '''Sample''' as it is displayed in the main window. You can also change the speed of animation. The default frame duration has a value of 300 (3x100) milliseconds. To stop the animation, simply press the keyboard's '''Esc Key'''.
+<table>
+<tr>
+<td> [[Image:Terrano pathloss.png|thumb|360px|Cartesian graph of path loss.]] </td>
+<td> [[Image:Terrano delay.png|thumb|360px|Bar graph of power delay profile.]] </td>
+</tr>
+<tr>
+<td> [[Image:Terrano ARR phi.png|thumb|360px|Polar stem graph of Phi angle of arrival.]] </td>
+<td> [[Image:Terrano ARR theta.png|thumb|360px|Polar stem graph of Theta angle of arrival.]] </td>
+</tr>
+<tr>
+<td> [[Image:Terrano DEP phi.png|thumb|360px|Polar stem graph of Phi angle of departure.]] </td>
+<td> [[Image:Terrano DEP theta.png|thumb|360px|Polar stem graph of Theta angle of departure.]] </td>
+</tr>
+</table>
-[[File:prop_run13.png]]    [[File:prop_run14.png]]
+=== Visualizing 3D Radiation Patterns of Transmit and Receive Antennas in the Scene ===
-Multiple coverage maps on the Navigation Tree at the end of a frequency sweep and starting an animation from the contextual menu.
+When you designate a "User Defined Antenna Pattern" as the radiator type of a transmitter set or a receiver set, EM.Terrano copies the imported radiation pattern data file from its original folder to the current project folder. The name of the ".RAD" file is listed under the '''3D Data Files''' tab of the data manager. Sometimes it might be desired to visualize these radiation patterns in your propagation scene at the actual location of the transmitter or receiver. To do so, you have to define a new '''Radiation Pattern''' observable in the navigation tree. The label of the new observable must be identical to the name of the ".RAD" data file. In addition, the Theta and Phi angle increments of the new radiation pattern observable (expressed in degrees) must be identical to the Theta and Phi angular resolutions of the imported pattern file. If all these conditions are met, then go to the '''Simulate Menu''' and select the item '''Update All 3D Visualization'''. The contents of the 3D radiation patterns are added to the navigation tree. Click on one of the radiation pattern items in the navigation tree and it will be displayed in the scene.
-[[File:prop_run15_tn.png]]
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon6.png|thumb|left|640px|The received power coverage map of the random city scene with a highly directional dipole array transmitter.]]
+</td>
+</tr>
+</table>
-Animation controls dialog in the project workspace.
+By Default, [[EM.Cube]] always visualizes the 3D radiation patterns at the origin of coordinates, i.e. at (0, 0, 0). This is because that radiation pattern data are computed in the standard spherical coordinate system centered at (0, 0, 0). The theta and phi components of the far-zone electric fields are defined with respect to the X, Y and Z axes of this system. When visualizing the 3D radiation pattern data in a propagation scene, it is more intuitive to display the pattern at the location of the transmitter or receiver. The Radiation Pattern dialog allows you to translate the pattern visualization to any arbitrary point in the project workspace. It also allows you to scale up or scale down the pattern visualization with respect to the background scene.
-=== Running a Parametric Sweep with SBR ===
+In the example shown above, the imported pattern data file is called "Dipole_Array1.RAD". Therefore, the label of the radiation pattern observable is chosen to be "Dipole_Array1". The theta and phi angle increments are both 1&deg; in this case. The radiation pattern has been elevated by 10m to be positioned at the location of the transmitter and a scaling factor of 0.3 has been used.
-[[File:prop_run24.png|thumb|300px|EM.CUBE's variable dialog]]
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon8.png|thumb|left|640px|Setting the pattern parameters in the radiation pattern dialog.]]
+</td>
+</tr>
+</table>
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon7.png|thumb|left|720px|Visualization of the 3D radiation pattern of the directional transmitter in the random city scene.]]
+</td>
+</tr>
+</table>
-[[File:prop_run23.png|thumb|250px|Dialog for defining new variables]]
+There is an important catch to remember here. When you define a radiation pattern observable for your project, EM.Terrano will attempt to compute the overall effective radiation pattern of the entire physical structure. However, in this case, you defined the radiation pattern observable merely for visualization purposes. To stop EM.Terrano from computing the actual radiation pattern of your entire scene, there is a check box in EM.Terrano's Ray Tracer Simulation Engine Settings dialog that is labeled '''Do not compute new radiation patterns'''. This box is checked by default, which means the actual radiation pattern of your entire scene will not be computed automatically. But you need to remember to uncheck this box if you ever need to compute a new radiation pattern using EM.Terrano's SBR solver as an asymptotic EM solver (see next section).
-In EM.CUBE, all the CAD object properties as well as certain source, material and mesh parameters can be assigned as [[variables]]. [[Variables]] are defined to control and vary the values of such parameters either for editing purposes or to run parametric sweep or [[optimization]]. Variable are defined using the '''[[Variables]] Dialog''', which can be accessed in the three ways:
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon9.png|thumb|left|640px|EM.Terrano's Run Simulation dialog.]]
+</td>
+</tr>
+</table>
-# By clicking the '''[[Variables]]''' [[File:variable_icon.png]] button of the '''Compute Toolbar'''.
+== Using EM.Terrano as an Asymptotic Field Solver ==
-# By selecting '''Compute''' [[File:larrow_tn.png]] '''[[Variables]]...''' from the Menu Bar.
-# Using the keyboard shortcut '''Ctrl+B'''.
-The [[variables]] dialog is initially empty. To add a new variable, click the '''Add''' button to open up the '''Add Variable/Syntax Dialog'''. In this dialog you have to type in a name for the new variable and choose a type. The default type is '''Uniformly Spaced Samples'''. You also need to specify the '''Start''', '''Stop''' and '''Step''' values for the variable. In the figure below, a variable called &quot;Tx_Height&quot; is defined that varies between 2 and 10 with equal steps of 2. This means the sample set {2,4,6,8,10}. When you return to the [[variables]] dialog, the syntax of the new variable is shown as 2:10:2. The last number in this syntax is always the variable step. In this example, this variable is going to be used to control the height of the transmitter in a propagation scene.
+Like every other electromagnetic solver, EM.Terrano's SBR ray tracer requires an excitation source and one or more observables for the generation of simulation data. EM.Terrano offers several types of sources and observables for a SBR simulation. You already learned about the transmitter set as a source and the receiver set as an observable. You can mix and match different source types and observable types depending on the requirements of your modeling problem.
-Next, you have to attach the variable to the CAD object. In this case, the CAD object is the point object that represents the transmitter's radiator. To attach a variable to a CAD object, open the object's property dialog and type in the name of the variable as the value of a property or parameter. In this case, the variable Tx_Height is going to control the Z-Coordinate of the point object. Once the value of the object parameter is replaced by the name of an already defined variable, it is updated with the current value of that variable. In the case of a variable of &quot;Uniformly Spaced Samples&quot; type, the current value is the start value. This value will be incrementally varied during a parametric sweep simulation process. Note that a variable can take a fixed value or a discrete set of values, too. You can always open the [[variables]] dialog and change the value or syntax of any variable. To make a new or modified value effective, click the '''Apply''' button of the [[variables]] dialog. You can test the values by performing a '''Dry Run''' of the selected variable. This runs an animation of the project workspace as the value of the variable changes and all the related CAD objects are updated accordingly. Note that you can attach the same variable to more than one CAD object property or to the properties of different objects. You can also define multiple values or syntaxes to the same variable. To do so, open the '''Add Variable/Syntax Dialog''', and instead of typing in a new variable name, choose an existing variable name from the '''Name''' dropdown list. This will add a new value or syntax to the existing syntax(es) of the selected variable. When you return to the [[variables]] dialog, [[variables]] with more than one value or syntax will have a dropdown list in the '''Syntax''' column. You can choose any of these values or syntaxed at any time and make the change effective by clicking the '''Apply''' button.
+The available source types in EM.Terrano are:
-[[File:prop_run25.png]]
+{| class="wikitable"
+|-
+! scope="col"| Icon
+! scope="col"| Source Type
+! scope="col"| Applications
+! scope="col"| Restrictions
+|-
+| style="width:30px;" | [[File:transmitter_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Point Transmitter Set | Point Transmitter Set]]
+| style="width:250px;" | Modeling realsitic antennas & link budget calculations
+| style="width:250px;" | Requires to be associated with a base location point set
+|-
+| style="width:30px;" | [[File:hertz_src_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Hertzian Short Dipole Source | Hertzian Short Dipole]]
+| style="width:250px;" | Almost omni-directional physical radiator
+| style="width:250px;" | None, stand-alone source
+|-
+| style="width:30px;" | [[File:huyg_src_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Huygens Source | Huygens Source]]
+| style="width:250px;" | Used for modeling equivalent sources imported from other [[EM.Cube]] modules
+| style="width:250px;" | None, stand-alone source imported from a Huygens surface data file
+|}
-Replacing the value of a CAD object parameter with a variable name.
+Click on each type to learn more about it in the [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types]].
-To run a parametric sweep, open the '''Run Dialog''' and select the '''Parametric Sweep''' option in the '''Simulation Mode''' drop-down list. If you have not defined any [[variables]] in the project, the box in the '''[[Variables]]''' row before the '''View''' will be red. You have to turn it into green before you can run a simulation. By clicking the '''View''' button, you can open up the [[variables]] dialog from here. Once you click the '''Run''' button, EM.CUBE performs a parametric sweep by incrementally varying the values of all the defined [[variables]] from their start to stop values at the specified steps and updating all the related CAD objects. After the completion of a parametric sweep simulation, as many coverage maps as the total number of variable samples are generated and added to the Navigation Tree under the receiver set's entry. You can click on each of the coverage maps and visualize it in the project workspace. You can also animate the coverage maps sequentially. To do so, right click on the receiver set's name in the Navigation Tree and select '''Animation''' from the contextual menu. To stop the animation, simply press the keyboard's '''Esc Key'''.
+The available observables types in [[EM.Terrano]] are:
+{| class="wikitable"
+|-
+! scope="col"| Icon
+! scope="col"| Source Type
+! scope="col"| Applications
+! scope="col"| Restrictions
+|-
+| style="width:30px;" | [[File:receiver_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Point Receiver Set | Point Receiver Set]]
+| style="width:250px;" | Generating received power coverage maps & link budget calculations
+| style="width:250px;" | Requires to be associated with a base location point set
+|-
+| style="width:30px;" | [[File:Distr Rx icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Distributed Receiver Set | Distributed Receiver Set]]
+| style="width:250px;" | Computing received power at a receiver characterized by Huygens surface data
+| style="width:250px;" | None, stand-alone source imported from a Huygens surface data file
+|-
+| style="width:30px;" | [[File:fieldsensor_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Near-Field Sensor Observable | Near-Field Sensor]]
+| style="width:250px;" | Generating electric and magnetic field distribution maps
+| style="width:250px;" | None, stand-alone observable
+|-
+| style="width:30px;" | [[File:farfield_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Far-Field Radiation Pattern Observable | Far-Field Radiation Pattern]]
+| style="width:250px;" | Computing the effective radiation pattern of a radiator in the presence of a large scattering scene
+| style="width:250px;" | None, stand-alone observable
+|-
+| style="width:30px;" | [[File:huyg_surf_icon.png]]
+| style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Huygens Surface Observable | Huygens Surface]]
+| style="width:250px;" | Collecting tangential field data on a box to be used later as a Huygens source in other [[EM.Cube]] modules
+| style="width:250px;" | None, stand-alone observable
+|}
+Click on each type to learn more about it in the [[Glossary of EM.Cube's Simulation Observables & Graph Types]].
+When you define a far-field observable in EM.Terrano, a collection of invisible, isotropic receivers are placed on the surface of a large sphere that encircles your propagation scene and all of its geometric objects. These receivers are placed uniformly on the spherical surface at a spacing that is determined by your specified angular resolutions. In most cases, you need to define angular resolutions of at least 1&deg; or smaller. Note that this is different than the transmitter rays' angular resolution. You may have a large number of transmitted rays but not enough receivers to compute the effective radiation pattern at all azimuth and elevation angles. Also keep in mind that with 1&deg; Theta and Phi angle increments, you will have a total of 181 &times; 361 = 65,341 spherically placed receivers in your scene.
-[[File:prop_run26.png]]
+{{Note| Computing radiation patterns using EM.Terrano's SBR solver typically takes much longer computation times than using [[EM.Cube]]'s other computational modules.}}
+<table>
+<tr>
+<td> [[Image:SBR pattern.png|thumb|540px|Computed 3D radiation pattern of two vertical short dipole radiators placed 1m apart in the free space at 1GHz.]] </td>
+</tr>
+</table>
-Choosing parametric sweep as the simulation mode in the run dialog. Note that one variable has been defined and EM.CUBE is ready to run the simulation.
+== Statistical Analysis of Propagation Scene ==
-[[File:prop_run27_tn.png|800px]]
+EM.Terrano's coverage maps display the received power at the location of all the receivers. The receivers together from a set/ensemble, which might be uniformly spaced or distributed across the propagation scene or may consist of randomly scattered radiators. Every coverage map shows the '''Mean''' and '''Standard Deviation''' of the received power for all the receivers involved. These information are displayed at the bottom of the coverage map's legend box and are expressed in dB.
-The coverage map of the scene at the end of a parametric sweep where the sweep variable is the transmitter height.
+When you run either a frequency sweep or a parametric sweep simulation in EM.Terrano, you have the option to generate two additional coverage maps: one for the mean of all the individual sample coverage maps and another for their standard deviation. To do so, in the '''Run Dialog''', check the box labeled '''&quot;Create Mean and Standard Deviation received power coverage maps&quot;'''. Note that the mean and standard deviation values displayed on the individual coverage maps correspond to the spatial statistics of the receivers in the scene, while the mean and standard deviation coverage maps show the statistics with respect to the frequency or other sweep variable sets at each point in the site. Also, note that both of the mean and standard deviation coverage maps have their own spatial mean and standard deviation values expressed in dB at the bottom of their legend box.
-=== Statistical Analysis of Propagation Scene ===
+<table>
+<tr>
+<td>
+[[Image:PROP MAN12.png|thumb|left|480px|EM.Terrano's simulation run dialog showing frequency sweep as the simulation mode along with statistical analysis.]]
+</td>
+</tr>
+</table>
-EM.CUBE's coverage maps display the received power at the location of all the receivers. The receivers together from a set/ensemble, which might be uniformly spaced or distributed across the propagation scene or may consist of randomly scattered radiators. Every coverage map shows the '''Mean''' and '''Standard Deviation''' of the received power for all the receivers involved. These information are displayed at the bottom of the coverage map's legend box and are expressed in dB.
+<table>
+<tr>
+<td>
+[[Image:UrbanCanyon4.png|thumb|left|640px|The mean coverage map at the end of a frequency sweep.]]
+</td>
+</tr>
+<tr>
+<td>
+[[Image:UrbanCanyon5.png|thumb|left|640px|The standard deviation coverage map at the end of a frequency sweep.]]
+</td>
+</tr>
+</table>
-In the [[Propagation Module]], when you ran a sweep simulation (frequency, transmitter or parametric), you also have the option to generate two additional coverage maps: one for the mean of all the individual sample coverage maps and another for their standard deviation. To do so, in the '''Run Dialog''', check the box labeled '''&quot;Create Mean and Standard Deviation Coverage Maps&quot;'''. Note that the mean and standard deviation values displayed on the individual coverage maps correspond to the spatial statistics of the receivers in the scene, while the mean and standard deviation coverage maps correspond to frequency, transmitter or variable sets defined for the sweep simulation. Also, note that both of the mean and standard deviation coverage maps have their own spatial mean and standard deviation values expressed in dB at the bottom of their legend box.
+<br />
-[[File:prop_run21_tn.png]]
+<hr>
-The mean coverage map at the end of a transmitter sweep.
+[[Image:Top_icon.png|30px]] '''[[EM.Terrano#Product_Overview | Back to the Top of the Page]]'''
-[[File:prop_run22_tn.png]]
+[[Image:Tutorial_icon.png|30px]] '''[[EM.Cube#EM.Terrano_Documentation | EM.Terrano Tutorial Gateway]]'''
-The standard deviation coverage map at the end of a transmitter sweep.
+[[Image:Back_icon.png|30px]] '''[[EM.Cube | Back to EM.Cube Main Page]]'''

Difference between revisions of "EM.Terrano"

Latest revision as of 17:59, 11 January 2021

Contents

Product Overview

EM.Terrano in a Nutshell

EM.Terrano as the Propagation Module of EM.Cube

Advantages & Limitations of EM.Terrano's SBR Solver

EM.Terrano Features at a Glance

Scene Definition / Construction

Wave Propagation Modeling

Data Generation & Visualization

Building a Propagation Scene in EM.Terrano

The Various Elements of a Propagation Scene

Organizing the Propagation Scene by Block Groups

Moving Objects Among Different Block Groups

Adjustment of Block Elevation on Underlying Terrain Surfaces

EM.Terrano's Ray Domain & Global Environment

Why Do You Need a Finite Computational Domain?

Understanding the Global Ground

Defining Point Transmitters & Point Receivers for Your Propagation Scene

The Nature of Transmitters & Receivers

Defining a Point Transmitter Set in the Formal Way

Defining a Point Receiver Set in the Formal Way

Modulation Waveform and Detection

A Note on EM.Terrano's Native Dipole Radiators

A Note on the Rotation of Antenna Radiation Patterns

Adjustment of Tx/Rx Elevation above a Terrain Surface

Discretizing the Propagation Scene in EM.Terrano

Why Do You Need to Discretize the Scene?

Generating the Facet Mesh

Running Ray Tracing Simulations in EM.Terrano

Running a Single-Frequency SBR Analysis

Changing the SBR Engine Settings

Polarimetric Channel Analysis

The "Near Real-Time" Polarimatrix Solver

EM.Terrano's Simulation Modes

Transmitter Sweep

Rotational Sweep

Mobile Sweep

Investigating Propagation Effects Selectively One at a Time

Working with EM.Terrano's Simulation Data

The Ray Tracing Solvers' Output Simulation Data

Visualizing Field & Received Power Coverage Maps

Visualizing the Rays in the Scene

The Standard Output Data File

Plotting Other Simulation Results

Visualizing 3D Radiation Patterns of Transmit and Receive Antennas in the Scene

Using EM.Terrano as an Asymptotic Field Solver

Statistical Analysis of Propagation Scene

Navigation menu

Search